Ingenieria de Procesos aplicada a la Biotecnología de Microalgas
3.7 - Optimización de cultivos discontinuos y semicontinuos usando modelos de crecimiento.
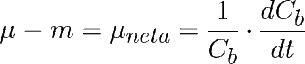
Vamos a utilizar el mismo caso que en el ejemplo anterior pero en discontinuo. FDe esta forma podemos comparar los resultados.
DISPONIBILIDAD DE LUZ
Ya sabemos el caso: geometría plana e incidencia perpendicular. La ecuación que da la disponibilidad la copiamos del ejemplo anterior (ka=0,19 m2g-1, Io=1500 mE m-2s-1 y L=0,05 m)
Ecuaciones
Vamos a optimizar un fotobiorreactor que va a funcionar por lotes. Asumimos buena mezcla (integración de irradiancias) e iluminación exterior constante.
El ejemplo es un fotobiorreactor plano de 5 cm de espesor y 500 L de volumen útil que se encuentra iluminado por 1500 mE m-2s-1 que incide perpendicularmente sobre el FBR.
Las propiedades ópticas de la biomasa son constantes y vienen definidas por ka=0,19 m2g-1.
Como modelo de crecimiento vamos a usar el de Camacho-Rubio con los parámetros µmax=0,045 h-1, α=180 µE m-2s-1, κ=0,075 y m=0,005 h-1.
Veamos las ecuaciones que rigen el ejemplo.
Definición del ejemplo
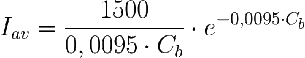
MODELO DE CRECIMIENTO
Vamos a usar el modelo de Camacho-Rubio con µmax=0,045 h-1, α=180 µE m-2s-1y κ=0,075.
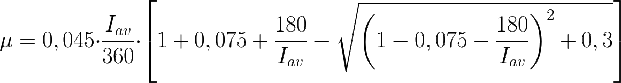
BALANCE DE MATERIA
El balance de materia es el caso del cultivo por lotes es:
Para este caso, lo despejamos como:
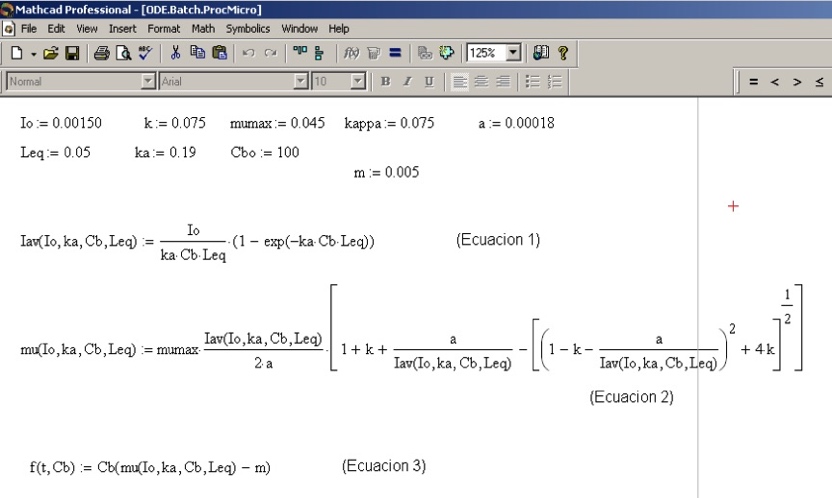
Ecuacion 1
Ecuacion 2
Ecuacion 3
La optimización consiste en encontrar la concentración de inóculo y el tiempo de cultivo que maximizan la productividad de biomasa media del periodo que se calcula con:
Optimización
Ecuación diferencial que tenemos que integrar con un método numético y unas condiciones iniciales Cb=Cbo para t=0. La integración nos da Cb(t) con la precisión temporal (dt) que fijemos en el método de integración,
Donde ts es el tiempo de servicio que tiene en cuenta el tiempo necesario para limpiar y reinocular y debería tener en cuenta también el liempo de la fase lag. En este caso yo le he puesto, un poco al tun-tun, ts=10 horas.
La optimización consiste en encontrar la concentración de inóculo y el tiempo de cultivo que maximizan la productividad de biomasa media del periodo que se calcula con:
El proceso sería:
● Imponer Cbo a t=0 (concentración de inoculación)
● Obtener Cb(t) integrando la ecuación 3 hasta la fase estacionaria.
● Obtener la productividad media en cada momento con la ecuación 4 y encontrar el máximo.
● Repetir para diferentes concentraciones iniciales Cbo hasta encontrar el máximo absoluto de productividad.
A continuación se muestra esta optimización realizada en MathCad. Se puede hacer con la hoja de cálculo (utilizando alguna chapuza que otra) pero es muy engorroso y largo. Veamos la solución en MathCAD:
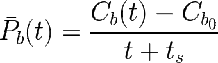
3.7 - Optimización de cultivos en discontinuo
Cuestiones
1 - Calcule el consumo total de nitrato (como nitrato sódico) en el caso optimizado (tf=55 h Cbo=800, Cbf=2245 g m-3). Calcule la concentración inicial necesaria de nitrato sódico en el sistema (CNaNO3(t=0)).
2 - Calcule el consumo instantáneo maximo de CO2. para el FBR propuesto (VR=0,5 m3) el el caso optimizado. El dato de máxima Pb instantánea se dará en clase.
3 - Calcule la producción máxima de O2 y la producción de O2 al principio (t=0) y al final de la fermentación (t=55) en el caso optimizado. Los datos de Pb instantanea se darán en clase.
4.- Calcule el volumen a cosechar en el caso optimizado (Cbf=2245 g m-3) de forma que al reponer este volumen con medio fresco le quede en el FBR una concentracion inicial de Cbo=800 g m-3). Operando de esta forma, estaría realizando un cultivo SEMICONTINUO.
Ecuacion 4
DEFINICIÓN DE VARIABLES Y ECUACIONES
Como puede comprobar, son las mismas variables y ecuaciones del ejemplo que venimos usando. Las unidades de irradiancia están en moles de fotones m-2 s-1 en vez de en µE o micromoles.
Ejemplo en MathCad
INTEGRACIÓN DE LA ECUACIÓN DIFERENCIAL
Se fijan las condiciones iniciales que son una concentración de 50 mg L-1 (50 g m-3) a tiempo cero (t0=0).
El bloque de resolución comienza con la palabra clave "Given". Inmediatamente se declara la ecuación diferencial que es el balance de materia.
A continuación viene la condición inicial Cb(0)=Cbo.
Finalmente, se usa el resolvedor "Odesolve" que integra la ecuación diferencial con la condición inicial guardandolo en la variable Cb(t), que es un vector o sucesión de valores numéricos.
La gráfica muestra la evolución de la concentración de biomasa en el cultivo batch durante el tiempo de cultivo fijado.
El tiempo final, tf, lo he fijado tanteando para que se acerque más o menos a la fase estacionaria.
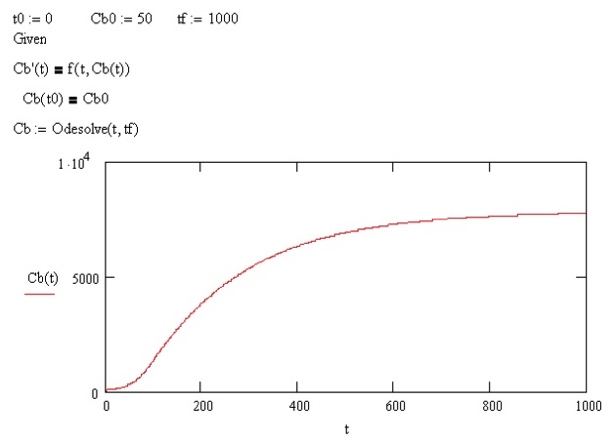
CALCULO DE LA PRODUCTIVIDAD MEDIA
Se calcula la productividad media en cada tempo de la fermentación como el increento de la concentración dividido por el tiempo total transcurrido.
Para evaluar la productividad del lote, tenemos que incluir el tiempo de servicio, ts, que es el tiempo que llevaría limpiar, inocular y tener el cultivo en fase exponencial otra vez. He fijado ts=10 h y tal vez me he quedado un poco corto.
Obtenemos que para Cbo=50 g m-3 de concentración inicial tenemos el máximo de productividad al cabo de unas 220 h con un valor de unos 18 g m-3 h-1.
Para un volumen de FBR de VR=500 L, habriamos obtenido unos 2 kg de bimasa (exactamente 1980 g).
Veamos si podemos obtener más.
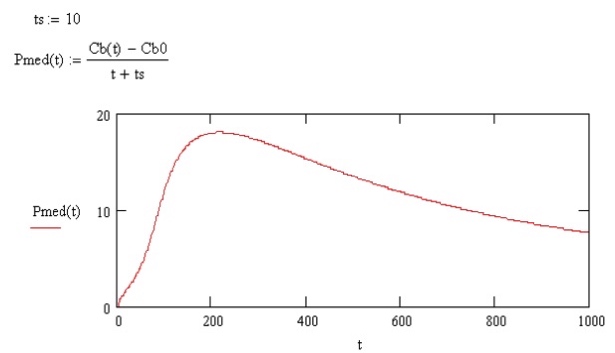
DIFERENTES CONCENTRACIONES DE INOCULACIÓN
Aunque no es el método más elegante, podemos repetir los dos pasos anteriores (integración y cálculo de la productividad media) con diferentes concentraciones iniciales Cbo.
Tanteando hasta que me he cansado, he obtenido los mejores resultados para Cbo=800 g m-3. No merece la pena afinar mucho más porque en este entorno de concentraciones iniciales (600-1000) se obtienen resultados casi iguales.
Con Cbo=800 g m-3 se obtiene un máximo de productividad de 23,626 g m-3 h-1 aproximadamente a las 65 h de cultivo (tf=65 h)
Para un volumen de FBR de VR=500 L, habriamos obtenido unos 767,8 g de biomasa en 65 h.
Comparandolo con el caso anterior, en 220 h nos daria tiempo a hacer 3,3 lotes que producirían 2598 g, como un 30% más. Habría que ver si compensa económicamente ya que el segundo caso tiene 3,3 veces más trabajo que el primero y eso cuesta dinero. Un problema típico de diseño de procesos.
CONSIDERACIONES ADICIONALES
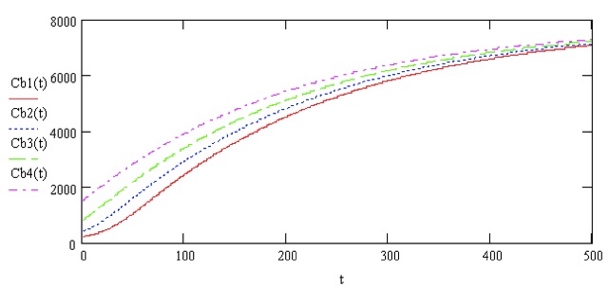
Ponemos la evolución de la biomasa con el tiempo en la gráfica de al lado para entender lo que pasa con cada Cbo ensayada y para:
● De la diferencia (Cbf-Cbo) podriamos calcular las necesidades de nutrientes. Por ejemplo, la concentración inicial necesaria de nitrato para un contenido en N de la biomasa del 5%.
● Si agregamos el nitrato en varias dosis a lo largo del tiempo de cultivo, tendriamos un sistema fed-batch.
A partir de la productividad instantánea Pbi=dCb/dt (no lo pongo por no agobiar, pero lo veremos en clase) podemos calcular:
● El consumo instantaneo de CO2 con los coeficientes del apartado 1-6. Este consumo instanténeo es la velocidad a la que debemos aportar CO2 al cutivo en cada momento.
● El máximo anterior fija la capacidad de transferencia de CO2 que debe tener el sistema para no producir limitación.
● Podemos calcular igualmente la generación de oxigeno instantanea y así averiguar la velocidad de eliminación de oxígeno necesaria y el máximo de esta velocidad que va a dar la capacidad de eliminación de oxígeno (kLa por volumen de intercambio) maxima necesaria.
Tanto la velocidad de aporte de CO2 como la de eliminación de O2 se pueden modifcar durante el cultivo fijando la concentración de CO2 en la aireación, modificando el volumen de aireación o la agitación, como aprenderá vd. en los temas que siguen.
El ejemplo en MathCad está aquí por si quiere modificar algo o completar los cálculos.