Ingenieria de Procesos aplicada a la Biotecnología de Microalgas
3.4 - Obtención de parámetros de crecimiento
La obtención de parámetros de crecimiento requiere tres pasos:
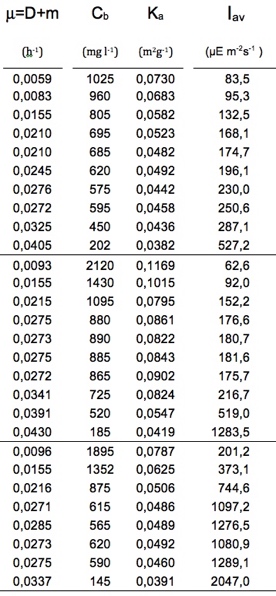
- Obtención de datos experimentales de µ vs. I (I es Iav en cultivos ópticamente densos).
- Selección del modelo de crecimiento.
- Obtención de los parámetros del modelo por regresión no lineal
El resultado es un modelo de crecimiento: una ecuación que da µ en función de la disponibilidad de luz y que permite optimizar el funcionamiento de lso fotobiorreactores maximizando su productividad.
A continuación mostramos algunos ejemplo de cómo seleccionar el modelo y de cómo tener en cuenta el efecto de la temeratura.
No hay ninguna receta mágica a la hora de escoger un modelo de crecimiento. Símplmente interesa más en que mejor sea capaz de correlacionar los datos experimentales.
En principio es preferible un modelo con un significado fisiológico ya que se puede saber si el valor de los parámetros es razonable.
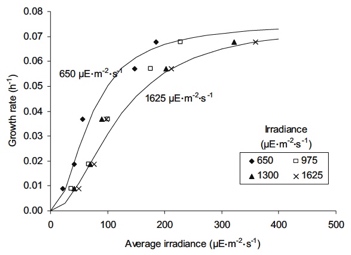
A la derecha se muestran experimentos en los que se ha medido µ en un cultivo en continuo que se ha dejado llegar al estado estacionario. A partir de Cb, ka y la geometría del fotobiorreactor, se ha calculado lo Iav correspondiente a cada estado estacionario.
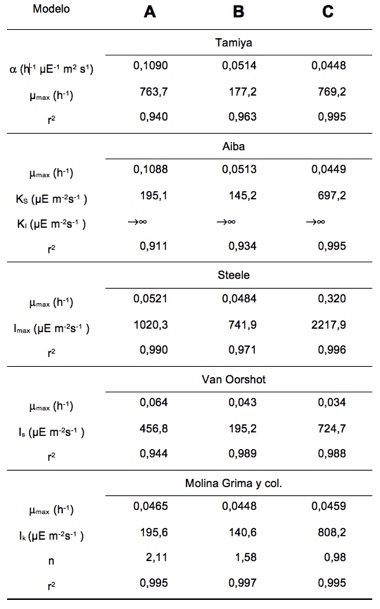
Selección de modelo: estudio estadístico ejemplo)
Este aspecto es quizás más importante que el coeficiente de determinación r2.
Por tanto, este caso no ofrece duda: escogeriamos el modelo de Molina y cols. de entre los probados, sin perjuidio de que pudiesemos ensayar alguno más. Sin embargo, pese al buen ajuste, la discrepancia de los parámetros Ik y n entre las series A, B y C (llevadas a cabo bajo diferente iluminación) nos obligan a usar diferentes parámetros para cada una de las series.
Influencia de la temperatura
A)
Io=800 µEm-2s-1
C)
Io=3200 µEm-2s-1
B)
Io=1600 µEm-2s-1
Para elegir el modelo de crecimiento más adecuado se ha realizado el estudio estadístico que se muestra a la izquierda: se han obtenido los parámetros correspondientes a los modelos de Tamiya, Aiba, Steele, Van Oorschot y Molina y cols.
Como se precia, el que mejores resultados ha dado ha sido el de molina y cols. y, por tanto, decidiriamos usar ese modelo.
También es importante que el modelo de Molina y cols ha dado resultados similares para el parámetro µmax en las tres series.
Esto es importante ya que, aunque el modelo de Molina y cols es empírico, µmax tiene significado fisiológico ( es la máxima velocidad de crecimiento) y cabe esperar que sea la misma en las tres series experimentales ya que se han realizado a la misma temperatura.
Este ejemplo muestra cómo obtener el modelo de crecimiento a partir de datos cinéticos y, en particular, llama la atención sobre el hecho de que la curva µ-I ypor tanto los datos cinéticos obtenidos, valen para la temperatura a la que han sido hechos los cultivos. La temperatura puede tener una fuerte influencia y debe obtenerse infrmación a todas las temperaturas a las que se vaya a trabajar.
En laboratorio esto no suele ser un problema, ya que se pueden termostatizar los cultivos y es lo que normalmente se hace para trabajar en el óptimo de temperatura. En el exterior y especialmente en cultivos grandes esto no es posible y es necesario introducir el efecto de la temperatura. El precio es que se neesita un conjunto de datos muy grande para poder construir varias curvas µ-I a varias temperaturas.
En el ejemplo que sigue se usan los datos de Sanchez y cols obtenidos para Scenedesmus almeriensis en cultivos en continuo en columnas de burbujeo de 2 L llevados a cabo en laboratorio a varias temperaturas (entre 10 y 45ºC) y a varias inrradiancias incidentes (entre 650 y 1625 µEm-2s-1). El trabajo usa el modelo de Molina y cols con una modificación para tener en cuenta la variación de Ik que, como se observa en los resultados, produce Io. También se observa que T influencia fundamentalmente la temperatura, por lo que se propone una ecuación (por analogía con otros microorganismos) para tener en cuenta la influencia de la temperatura en µmax.
A continuación se muestra un resumen gráfico del proceso de obtención del modelo.
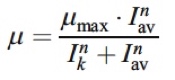
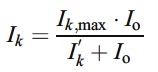
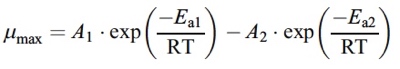
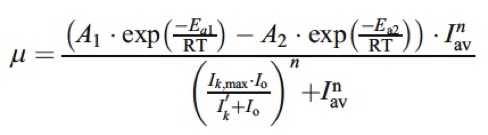
3.4 - Obtención de parámetros de crecimiento
Cuestiones
1 - Puede obtener los parámetros de crecimiento para el modelo de Camacho-Rubio a partir de los datos de la tabla 1 e incorporarlos a la Tabla 2.
2 - Comente la variación de los parámetros del modelo de Molina y cols. con Io.
REFERENCIAS
Biomass and lutein productivity of Scenedesmus almeriensis: influence of irradiance, dilution rate and temperature J. F. Sanchez & J. M. Fernandez-Sevilla & F. G. Acien & M. C. Ceron & J. Perez-Parra & E. Molina-Grima
Appl Microbiol Biotechnol (2008) 79:719–729 DOI 10.1007/s00253-008-1494-2
Tabla 1
Tabla 2
Obtención de datos
● Diferentes Io
● Diferentes T
● Cultivo continuo
● D=µ+m
● Resultado : Cb en estado estacionario.
● Permite calcular Iav
Análisis de regresión
Observaciones
● Ik varía con Io
● µ varía con T
Se proponen modificaciones:
Usar:
Para representar la variación de Ik con Io
Usar:
Para representar la variación de µ con T Ik con Io
Ecuación modificada
Análisis de regresión
Parámetros del modelo modificado
A1=3,20·105 (h-1)
Ea1=3,35·104 (J mol-1)
A2=1,44·1012 (h-1)
Ea2=7,85·104 (J mol-1)
n= 2,28
Ik,max=202 (µE m-2s-1)
I'k=726 (µE m-2s-1)
r2=0,8685
Con este modelo se puede predecir µ para Scenedesmus almeriensis en una amplia gama de circinstancias que incluye desde una temperatura muy baja (para ciltivos de mocroalgas (T=10ºC) hasta 45ºC qye está cerca de la temperatura de muerte de la cepa (que se estima en 47ºC).
Cuantas más circunstancias se incluyen, más difíciles de manejar y largas se vuelven las ecuaciones de crecimiento.
Dentro de lo posible, es preferible usar modelos adaptados a las condiciones de cultivo (T, Io y pH óptimos). Además de ser más fáciles de tratar, requieren menos trabajo experimental que en esta caso es muy importante.
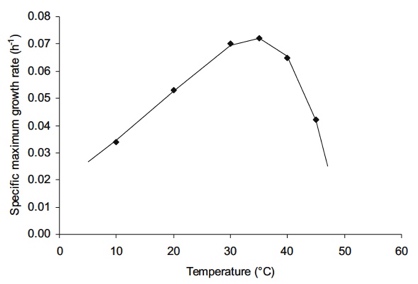
µmax vs T
A modo de ilustración se muetra la variación de µmax con T.
Como es típico en microorganismos y en reacciones bioquímicas, se presenta un máximo a temperaturas moderadas.
En este caso Tmax=35ºC.
µmax se mantiene alta entre 30ºC y 40ºC.
Después desciende muy rápidamente al aproximarse a la temperatura de muerte térmica que, como ocurre en muchos seres vivos, no se encuentra muy lejos de la T óptima.
