Ingenieria de Procesos aplicada a la Biotecnología de Microalgas

3.2 - Modelos estáticos de crecimiento fotolimitado para microalgas

Los modelos estáticos establecen una función entre la iradiancia I y la velocidad específica de crecimiento µ. Lo característico de los modelos estáticos es que son independientes del tiempo y por tanto el tiempo no aparece en la ecuación. Existen diferentes ecuaciones propuestas que varian fundamnetalmente en la forma de la curva µ-I. Algunas crecen más deprisa, son más rectas o más curvas o tienen forma sigmoidal.

Algunas son ecuaciones empíricas y otras surgen de mecanismos de reacción propuetos. El objeto de presentar las siguientes ecuaciones es disponer de la forma más adecuada para los datos experimentales, de manera que se pueda realizar una regresión adecuada.

Veamos algunas ecuaciones. No se olvide que si nonguna le satisface siempre puede proponer una propia.

La ecuación de Tamiya es una relación hiperbólica de µ frente a la irradiancia, que puede venir dada por I o por Iav. La ecuación originalmente propuesta por Tamiya en 1953 es:

Modelo de Tamiya

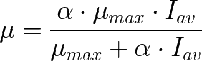
Que tiene dos parámetros. Uno de ellos es la µ maxima que controla el valor máximo al que llega µ.

El otro parámetro, α, regula la forma de la curva. Yo prefiero escribir esta ecuación dividiendo numerador y denominador por α, de forma que queda:

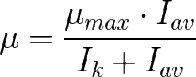
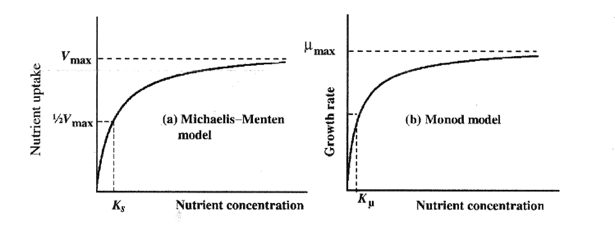
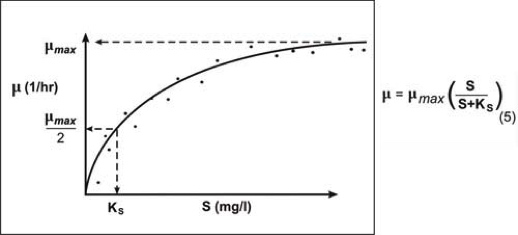
De esta forma se evidencia el parecido con el modelo de Michaelis-Menten para la cinética enzimática y con el modelo de Monod para el crecimiento de microorganismos.

Ik es un parámetro de forma que se puede definir como la irradiancia que hace µ=µmax/2.

Modelo de Blackmann

Uno de los defectos del modelo de Tamiya es que el incremento de µ es curvo y demasiado lento, cuando la realidad es que en las curvas de fotosíntesis se observa una fase lineal de µ frente a I seguida de una rápida saturación. Blackmann optó por definir una función en dos trams reogiendo esta característica. La definición es la siguiente:

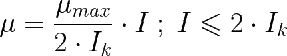
La formulación original del modelo es para microorganismos y está puento en función de la concentración de sustrato [S] en vez de la irradiancia. Lo he escrito con I pero casi siempre lo utilizaremos con Iav. De hecho, a este modelo a veces se le llama solo el "modelo discontinuo" ya que Blackmann nunco lo propueso para microalgas ni contempló I o Iav como sustrato.

Modelo de Van-Oorschot

Van-Oorschot propuso un modelo exponencial cuyo comportamiento se encuantra entre el de Tamiya y el de Blackmann. La ecuación es la siguiente:

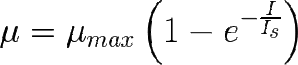
Donde Is es una constante de saturación. No la he llamado Ik porque no es exactamente igua en el sentido de que no define la irradiancia a la que  µ se hace µmax/2.

La ecuación propuesta por Van-Oorschot es similar al modelo para el crecimiento de microorganismos propuesto por Teissier.

El model de Van-Orschot es una curva suave, a diferencia del de Blackmann, pero crece rápidamente y alcanza µmax de forma relativamente rápida, a diferencia del modelo de Tamiya.

(Tamiya)

(Van-Oorschot)

Modelo de Molina

Los modelos anteriores son sencillos porque sólo tienen dos parámetros. Rsto es deseable porque los hace sencillos. Sin embargo son poco flexibles ya que no es posible variar la forma de la curva, sólo el máximo y la velocidad del incremento. Esto puede solucionarse con la inclusión de un parámetro de "forma" como en el caso del modelo de Moser propuesto para microorganismos. Molina y Cols. propusieron un modelo análo en el que µ es funcion de I o Iav en vez de ser función de la concenyración de sustrato [S]. La ecuación es:

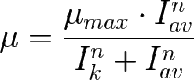
Que como se ve tiene 3 parámetros. µmax e Ik tienen el mismo significado que en el modelo de Tamiya, mientras que n es un parámetro de forma que da forma sigmoidal cuando n>1, como se puede ver en la gráfica de la derecha.

(Molina)

Modelo de Bannister

Bannister propuso otro modelo de 3 parámetros. Es una ecuación empírica. Tiene la ventaja de que presenta un tramo lineal que es típico de la fotosíntesis. La ecuación es:

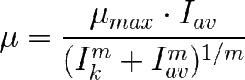
Las he escrito ambas con Iav porque es como más la usamos. Como se ve en la gráfica superior, se diferencia de la de Molina en su tramo recto, frente a la forma sigmoidal de la de Molina, pero son tan similares que puede ser dfícil distinguir cual representa mejor la relación µ-Iav.

La ecuación de Bannister fue propuesta para la fotosíntesis inicialmente, no habiendo un modelo similas para microorganismos o cinética enzimática.

Modelo de Camacho-Rubio

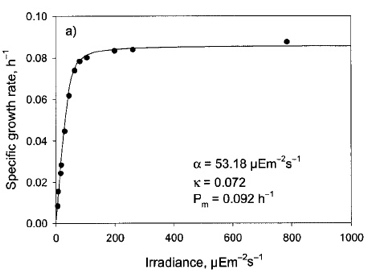
Tambien es un modelo de tres parámetros pero, a diferencia de las anteriores propuestas, proviene de un modelo mecanístico de la fotosíntesis formulado explicitamente para el crecimiento microalgal. El modelo de Camacho-Rubio (2013) es:

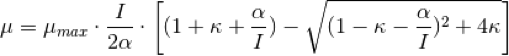
El significado de µmax es análogo al que aparece en las demás ecuaciones. Los otrs dos parámetros α y κ, son una constante de saturación y un parámetro de forma.

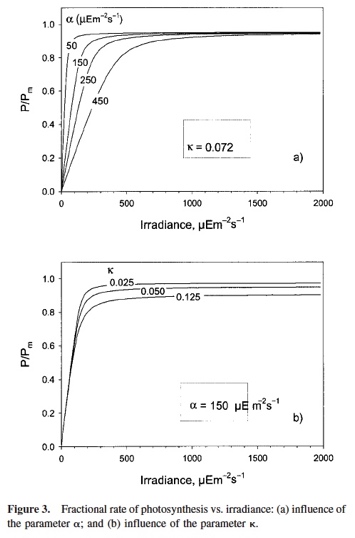
En la gráfica de la derecha puede verse el comportamiento del modelo respecto de estos parámetros. α influencia la velocidad con la que aumenta µ con I y lo rápido que se satura. Cuando I=α, µ está muy cerca de µmax (a diferencia de Ik, que hacia µ=µmax). κ, influencia la brusquedad de la transición de la fase lineal a la saturación. κ bajo da transiciones bruscas y viceversa.

Debajo se muestran los parámetros obtenidos para unos datos experimentales como ejemplo de los valores que pueden tomar estos parámetros.

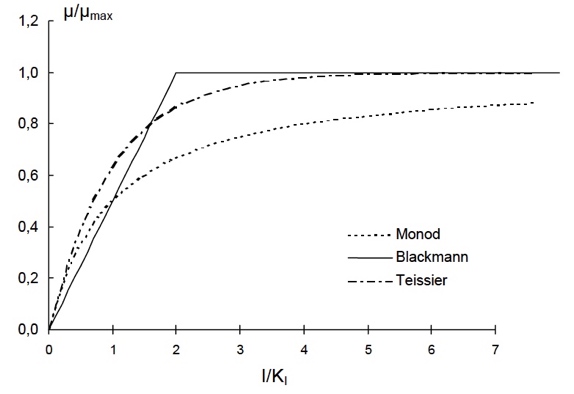
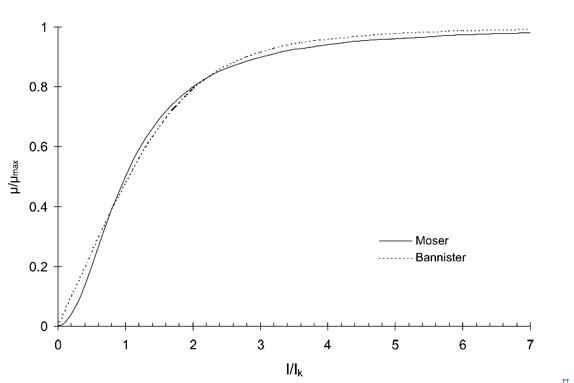
Otros modelos

Se han propuesto otros modelos que vd. sólo necesitaría considerar en el caso de que ninguno de los anteriores fuese capaz de correlacionar bien sus datos. A la derecha se muestran algunos ejemplos que no tienen mayor transcendencia.

Si hiciesemos una busqueda bibliográfica seguro que encontraríamos muchas más propuestas.

3.2 - Modelos estáticos de crecimiento fotolimitado

Cuestiones

1 - Encuentre para todos los modelos cuando ocurre que µ=µmax/2.

2 - ¿Que ocurre con el modelo de Camacho Rubio cuando κ=0?

3 - La µ de estos modelos ¿es bruta o neta?

4 - ¿Que influencia tiene la temperatura en esto modelos? ¿Cómo podría tenerse en cuenta?

REFERENCIAS

Van Oorschot, J.L.P. (1955) Conversion of Light Energy in Algal Cultures, Med. van. Lund. Wang. 55: 225‑277

Bannister, T.T. (1979) Quantitative description of stedy state, nutrient-saturated algal growth, including adaptation. Limnol. Oceanogr. 24(1): 76-96

Blackman F.F. (1905) Ann. Bot 19:281

Molina Grima E., Sánchez Pérez J.A., García Camacho F., García Sánchez J.L., López Alonso D. (1993) n-3 PUFA productivity in chemostat cultures of microalgae. Appl. Microbiol. Biotechnol: 38: 599-605

Moser A. (1985) Kinetics of Batch Fermentation, en Biotechnology Vol. 2, H.J. Rehm y G. Reed (Ed.),VCH Verlagsgesellschaft mbH Weinheim Germany. 243‑283

Monod J. (1942) Recherches sur la croissance des cultures bacteriennes. Herman & cie. Paris

Tamiya H., (1953) Mass Culture of Algae, Ann. Rev. Plant Physiol., 8, 309.