Ingenieria de Procesos aplicada a la Biotecnología de Microalgas
3.5 - Modelos dinamicos de crecimiento
Vamos a presentar los modelos dinámicos de crecimiento con el único objetivo docente de definirlos, pero no los vamos a usar para el diseño de FBRs en este curso de introducción.
Para el diseño en este curso siempre asumiremos que estamos en una situación de integración de la irradiancia (µ=µ(Iav)) y, aunque no tienen nada que ver con el contenido de este apartado, sin fotoinhibición. Si no fuese así, cambiariamos el diseño para evitar cualquiera de estas limitaciones, agitando más, sombreando o de cualquier otra forma.
Cuando encendemos la luz con una irradiancia I, no se observa inmediatamente la actividad fotosintética que le correspondería, µ(I), si no que lleva un tiempo que puede ser de varios minutos alcanzar el valor que predice el modelo.
Igualmente, si tenemos establecidas unas condiciones de fotosíntesis µ(I1) y cambiamos a otras condiciones de luz, I2, también se observa un retraso en el establecimiento de la intensidad de la fotosíntesis correspondiente a las nuevas condiciones µ(I2).
Por tanto, los modelos estaticos de la fotosíntesis no reproducen los cambios de luz. Si tenemos una irradiancia variable I(t), una ecuación como el modelo de Tamiya re escrita de la forma:
Irradiancia variable
No representa bien la realidad. Si I(t) varia muy lentamente, como ocurre con la variación de la intensidad de luz del Sol a lo largo del dia, los modelos estáticos dan una respuesta más o menos correcta, pero ante cambios más rápidos, como los que nienen lugar cuando las microalgas se mueven entre zonas iluminadas y oscuras en un cultivo denso, la respuesta de los modelos estáticos será erronea todo el tiempo.
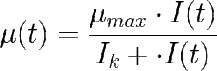
Como ya hemos dicho en el apartado 3.1, los modelos estáticos en cultivos densos sólo son aplicables a dos circusntancias extremas: cultivos completamente estáticos (integración de velocidades locales) y perfectamente mezclados (integración de irradiancias), que venían definidas por el factor de integración:
Modelos estáticos en cultivos densos
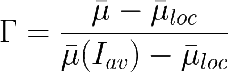
Que varía entre Γ=0 para la situación de integración de velocidades locales (µ=µloc) y la integración de irradiancia Γ=1 (µ=µ(Iav)).
Esto pone de manifiesto que son posibles situaciones intermedias que no podemos analizar. Y lo que es más, queda la cuestión de cuanta agitación es suficiente para conseguir una situación de integración de irradiancias, que es la situación más beneficiosa en todos los aspectos
Ya hemos comentado varias veces que en cultivos densos coexisten zonas oscuras e iluminadas. No solo eso.
Sabemos que la variación de la luz entre zonas es una distribución continua que venimos denominando distribución de irradiancias y que denotamos como:
I(x,y,z)
Crecimiento de microalgas en cultivos densos: el patrón de irradiancias I(t)
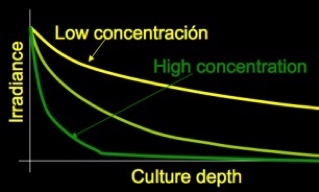

Hemos aprendido a obtener I(x,y,z) en varias circunstancias.
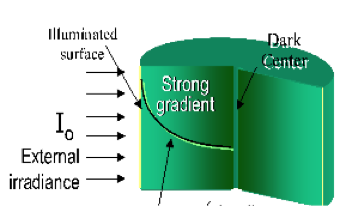
También hemos mencionado que la agitación es imprescindible en los cultivos de microalgas. Esta agitación provoca un movimiento que podemos representar por su posición p(t)=(x(t),y(t),z(t)), como se representa en el esquma de abajo:
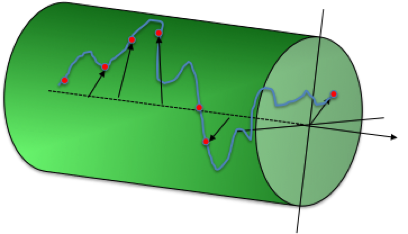
Es decir, tenemos simultaneamente presentes una distribución de irradiancias I(x,y,z) y un movimiento p(t)=(x(t),y(t),z(t)) que se superponen.
En consecuencia, el elemento de fluido que se mueve, y las microalgas que transporta, están sometidas a una irradiancia variable como se recoge en el esquema inferior:
p(t)
I(x,y,z)
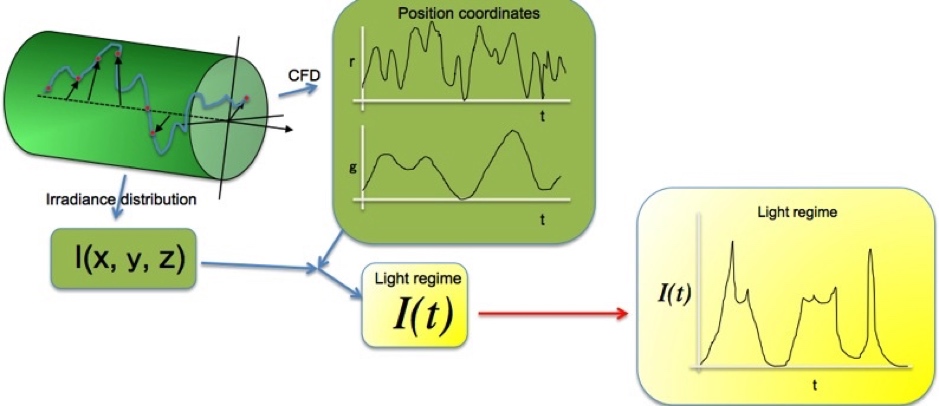
Por tanto, las microalgas "ven" una irradiancia variable
I(t)
que denominamos "patrón de irradiancias" o "régimen de luz" y en ambos casos hace referencia a cómo se recibe la luz.
El patrón de irradiancias contiene infrmación tal como el máximo de irradiancia que se ve, Imax, la frecuencia de las transiciones luz/oscuridad y si predominan las zonas oscuras y las iluminadas.
Modelos dinámicos de crecimiento
En un cultivo sin zonas muertas ocurre que:
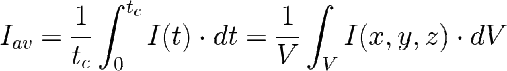
Para un tc lo suficientemente largo. Cuanto menor sea al tc, mejor mezclado está el cultivo y más posibilidades tenemos de estar en una situación de integración de irradiancias µ=µ(Iav).
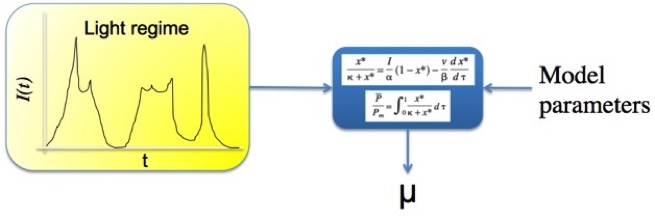
A diferencia de los modelos estáticos, los modelos dnámicos son capaces de aceptar la información de irradiancia como un patrón temporal I(t) y predecir una respuesta.
El modelo da la respuesta pertinente si la situación es de integración de irradiancias o de velocidades locales y, por supuesto, dan la respuesta en situaciones intermedias,
Los modelos dinámicos son ecuaciones diferenciales en función del tiempo que que contienen los parámetros de crecimiento del microorganismo y han de ser integrados con el patrón de irradiancias del dispositivo (fotobiorreactor) en el que se realiza el cultivo.
Veremos dos modelos dinámicos.
Modelo de Eilers & Peeters
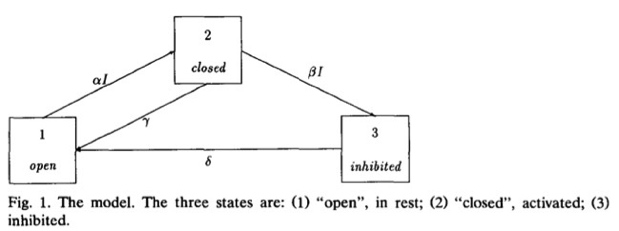
En 1993, Eilers & Peeters propusieron un conjunto de ecuaciones diferenciales que cuantificaman lo que ocurre en un modelo simplificado de la fotosíntesis. El modelo de la fotosíntesis propuesto fue:
Que postula que los cetros fotosinteticos (PSU) no activados (open) se activan tras la absorción de luz (pasan a activados o closed) y el proceso de desactivación en el que causa la fotosíntesis y con ello la generación de O2 y la generación de nueva biomasa.
La velocidad de activación de centros es proporcional a la concentración de centros desactivados (x1), a la intensidad de la luz (I) y a un coeficiente (α).
La velocidad de desactivación, y por tanto la de la fotosíntesis, viene dada por el producto x2·γ, la concentración de dentros activados por un coeficiente de velocidad.
El modelo contempla también un mecanismo de fotoinhibición (βI) y regeneración (δ) del que no vamos a dar más detalles.
El modelo se concreta en las siguientes ecuaciones:

Que pueden integrarse siempre que se conozca el patrón de luz I(t) y los parámetros de crecimiento del microorganismo α, β, x2·γ y δ.
Se han obtenido ecuaciones algebraicas integradas para este modelo para casos simples de I(t) como iluminación constante (I(t)=Io), pero no vamos a pomer ninguna porque no lo vamos a usar.
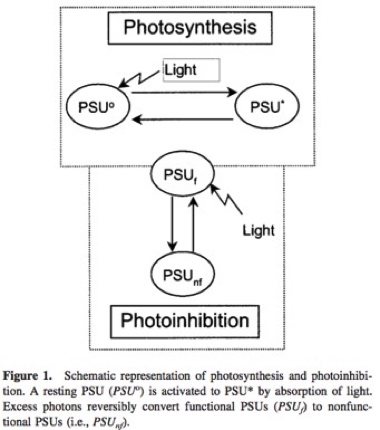
Modelo de Camacho-Rubio
En 2003, Camacho-Rubio propone un modelo similar al de Eiler y Peeters pero con la modificación de que el proceso de consumo de centros activados no es un proceso de primer orden, sino una reacción enzimática controlada por una ecuación tipo Michaelis-Menten:

3.5 - Modelos dinámicos de crecimiento
Cuestiones
1 - Compare los modelos de Eilers y Peeters y Camacho-Rubio. Intente encontrar similaridades y diferencias entre los parámetros.
2 - Escriba las ecuaciones de ambos modelos sin fotoinhibición. ¿En ue condiciones son iguales ambos modelos?
REFERENCIAS
CamachoRubio,F.,Garcia Camacho,F.,Fernandez Sevilla,J.M.,Chisti,Y.,Molina Grima, E., 2003. A mechanistic model of photosynthesis in microalgae. Biotechnol. Bioeng. 81, 459–473.
Eilers PHC, Peeters JCH. 1993. Dynamic behaviour of a model for photosynthesis and photoinhibition Ecol Modelling 69:113–133.
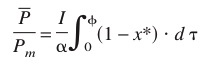
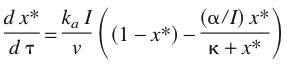
donde x* es la ftacción de centros activados que se generan co la iluminación y se consumen en el metabolismo. La respuesta fotosintética media viene dada por la integral:
No vamos a dar más detalles pero si le hace falta puede acudir a la referencia. Sí comentaremos que el modelo puede simular situaciones intermedias entre la integración de irradiancias y la de velocidades locales como demuestra el análisis del factor de integración:
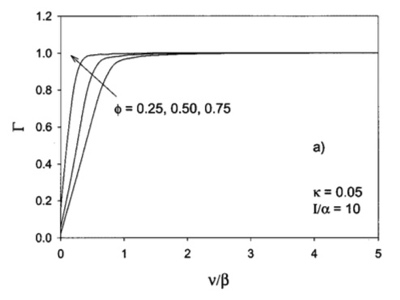
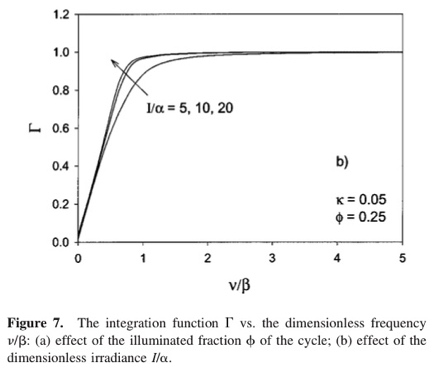
A continuación mostramos un ejemplo en MathCad en el que se calcula el factor de integración en varias circunstancias.
