Ingenieria de Procesos aplicada a la Biotecnología de Microalgas
2.3 - Transmisión de la luz en diferentes geometrías
Recuerde que para poder simplificar el complejo problema de la transmisión de la radiación que viene definido por la ecuacion de Boltzmann:
Es lo que vamos a calcular en este epígrafe.
El campo de irradiancias luego nos permitira calcular un promedio espacial de la irradiancia que es el número que nos dará la disponibilidad de luz en un cultivo.
Como hemos dicho, para calcular la atenuación tenemos que calcular el camino óptico p(x,y,z,...) de cada haz que llega a un punto del interior del cultivo. Para ello, necesitamos considerar dos elementos: geometría y modelo de transmisión de luz.
Geometría
La geometría va a ser muy sencilla. Sólo vamos a considerar los casos de geometría plana y cilíndrica porque cubren todos los fotobiorreactores que podemos encontrar. Algunos cultivos de laboratorio se realizan en matraces esféricos, pero dado su escaso interés, por simplicidad lo vamos a ignorar. Las geometrías estudiadas son, por tanto:
- Geometría PLANA : como FBRs planos y raceways.
- Geometría CILINDRICA : como columnas o FBRs tubulares.
Modelo de transmisión de la luz.
Hace referencia cómo llega la luz a cada punto. En principio la irradiancia (que es una suma de todas las direcciones) puede llegar de todas las direcciones y preferentetemente más de unas que de otras. La descripción rigurosa de éto es una función llamada radiancia R(x,y,z,ø,φ) que dice la luz que llega a cada punto (x,y,z) y de dónde llega (ø,φ). La irradiancia es el resultado de integrar R en todas las direcciones del espacio (ø,φ).
Esto es demasiado complicado. Nosotros vamos a distinguir sólo las circunstancias más habituales, que son el flujo colimado o directo y el difuso.
Campo de irradiancias I(x,y,z)
Hemos tenido que despreciar la dispersión (lo que no está demasiado mal en cultivos de microalgas) y describir solo la propagación unidimensional en haces. Entonces la atenuación venia dada por la ecuación de Lambert-Beer:
El precio que se paga por esta simplificación es que tenemos que describir "a mano" el camino que recorren los haces que llegan a un punto (x,y,z) en el inerior del cultivo para calcular el campo de irradiancias I(x,y,z).
Flujo colimado o directo.
Lo caracteristico es que los haces que alcanzan un punto llegan de una sola dirección. Esto pasa con el Sol o, en general, con fuentes puntuales en el infinito (o bastante lejos del cultivo). El el caso del Sol el flujo es DIRECTO PARALELO, porque los rayos o haces van paralelos unos a otros.
Existen otros flujos colimados como puede ser el flujo colimado RADIAL. En este caso, todos los haces van hacia el centro del cilindro. Este caso pasa con, por ejemplo, reflectores parabólicos. Lo he puesto de ejemplo porque se han construido dispositivos así pero no deja de ser un caso poco usual.
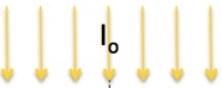
Flujo difuso.
En el flujo difuso se acepta que los haces de fotones que alcanzan un punto llegan de todas las direcciones del espacio. Nosotros vamos a asumir para simplificar que dichas direcciones están restringidas a un plano.
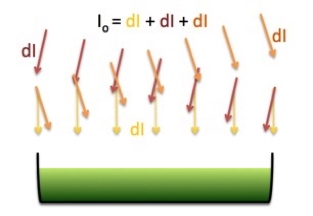
La figura de debajo muestra un sistema al que la luz llega desde 3 direcciones. Imagínese que llega desde infinitas direcciones y tendrá una visión de lo que es el flujo difuso. De cada dirección ø llega, por supuesto, un diferencial de I que es dI=(Io/2π)·dø si llega desde todas las direcciones o dI=(Io/π)·dø si llega sólo de un hemisferio.
Flujo directo (o colimado) paralelo
Flujo parcialmente difuso en un sistema plano.
A continuación vemos los casos más habituales.
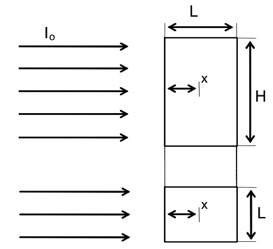
Flujo directo perpendicular
Sea una cubeta plana (podria ser un FBR plano). Este caso es muy sencillo. De la gráfica se deduce el camino óptico. Aceptando que la atenuación de luz viene dada por Lambert-Beer, la irradiancia en cualquier punto interno I(x,y,z) es:
Geometría plana, flujo directo.
Esta nos suena. Dice que I sólo dpende de x, la distancia entre el punto interior y la superficie. Como las otras variables de posición (y,z) no influyen para nada, no las ponemos,
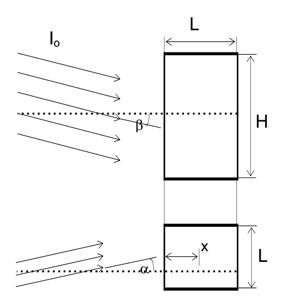
Flujo directo inclinado
Si el flujo incide con un ángulo α (en la figura pone beta, pero yo voy a usar alfa) medido como la desviación desde la perpendicular, el camino óptico de un punto alejado x de la superficie de incidencia se alarga convirtiendose en:
Y, por tanto:
Flujo directo perpendicular
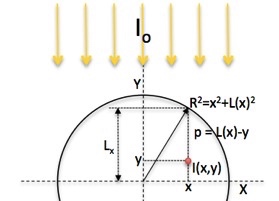
En este caso, como se deduce de la figura, el camino óptico depende de dos coordenadas. En un sistema cartesiano (podria haberlo puesto en cilíndricas) el camino óptico es:
Geometría cilíndrica, flujo directo.
Por tanto:
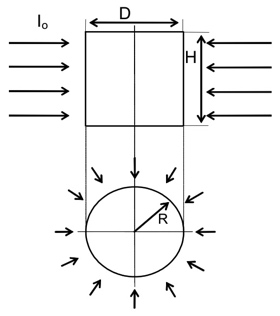
Flujo radial
Hace falta un balance de flujo que no voy a presentar y que tiene en cuenta que el flujo se va concentrando hacia el centro, como se ve en el equema del flujo radial presentado más arriba. La ecuación que de I con la posición radial es:
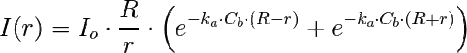
En este caso, como se deduce de la figura, I llega como contribuciones diferenciales dIo=Io/π·dα desde infinidad de direcciones desviadas de la perpendicular entre -π/2 y π/2. Siendo x la distancia entre el punto y la superficie de incidencia, el camino óptico es:
Geometría plana, flujo difuso.
Y cada contribución diferencial llega atenuada según:
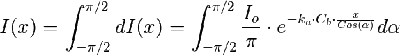
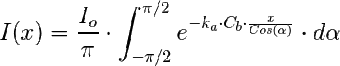
Que ha de evaluarse numéricamente.
Hacer para la geometría cilíndrica lo mismo que hemos hecho para la plana es difícil, lioso y largo. Afortunadamente, Evers en 1991 publico una manera de evaluar el camino óptico p de un haz que incide con un álgulo ø en un punto que se encuentra a S bajo la superficie.
Sin entrar en más cosnideraciones, usando el esquema propuesto por el autor, el camino óptico p(S,ø) resulta:
Geometría cilíndrica, flujo difuso.
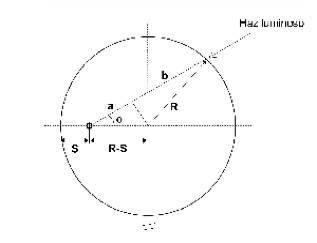
Y, análogamente a lo que hemos hecho para la geometría plana, la suma de contribuciones es:
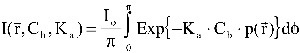
Esto es la nomenclatura original del autor. Puesto con las mismas variables que venimos usando nosotros, quedaría algo como:
Con estas ecuaciones podremos evaluar la disponibilidad de luz, el promedio Iav, que nos será muy util en el análisis cinético y que es en realidad el principal interés por el que hemos sacado estas ecuaciones.
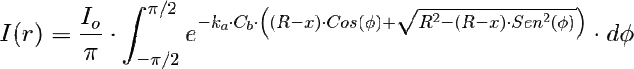
Cuestiones
1 - Calcule la irradiancia en el centro de una cubeta (geometría plana) de L= 8 cm iluminada perpendicularmente por irradiancia directa de Io=1200 µE m-2 s-1. La cubeta está llena con cultivo de Cb=1,5 g/L con ka=0,25 m2/g
2 - Repita la cuentión anterior sabiendo que la luz incide con un ángulo de 40º.
3 - Calcule la irradiancia en el centro de una columna iluminada con irradiancia directa de Io=1000 µE m-2 s-1 sabiendo que contiene un cultivo de Cb=1,8 g/L con ka=0,2 m2/g.
4 - Repita la cuestión anterior suponiendo un modelo de irradiancia difuso.
5 - Dibuje el perfil de irradiancia a intervalos de 1 cm para la cuestión anterior.
2.2 - Transmisión de la luz en diferentes geometrias
REFERENCIAS
Evers E. G., (1991). A model for light-limited continuous cultures: growth, shading, and maintenance. Biotechnology and Bioengeneering. 38: 599-605
Alfano, O.M., Romero, R.L. and Cassano, A.E. (1986a) Radiation field modelling in photoreactors-I. Homogeneous media. Chem. Eng. Sci. 41: 421-444
Alfano, O.M., Romero, R.L. and Cassano, A.E. (1986b) Radiation field modelling in photoreactors-II. Heterogeneous media. Chem. Eng. Sci. 41: 445
Zolner III, W.J. and Wlliams, J.A. (1971) Three-dimensional light distribution model for an elliptical photoreactor. A.I.Ch.E. J. 17: 502-503
NOTA: Hay que distinguir el modelo de transmisión según cada fuente. Por ejemplo:
- La luz solar es originalmente directa pero al pasar por la atmosfera aparece una componente difusa mayor o menor según lo "nublado" que esté.
- Las luces halógenas son directas.
- Los tubos fluorescentes dan luz mayoritariamente difusa.
- El albedo (luz reflejada por superficies no pulimentadas, incluyendo suelo y paredes blancos) es difusa.
El total de la irradiancia en el punto x se obtiene sumando las contribuciones:
Esto es:
