Ingenieria de Procesos aplicada a la Biotecnología de Microalgas
1.5 - Cultivos por lotes, continuos y semicontinuos
"Modo de cultivo" se refiere a la forma en la que se inocula y opera un PBR. Necesitamos entrar en estos detalles porque para seguir analizando los cultivos de microalgas necesitamos poder plantear los balances de materia que nos permiten obtener expresines para µ y, sobre todo, para Pb en función del tiempo, de forma que podamos predecirlas en función de las variables de operación.
Los modos de cultivo son tres:
- Discontinuo, por lotes o batch.
- Continuo
- Semicontinuo
Existe otra modalidad denominada fed-batch que consiste en añadir nutrientes periodicamente para evitar su agotamiento, pero nosotros de momento lo ignoraremos porque en el caso de las microalgas el nutriente limitante es la luz y esta llega al cultivo siempre de forma continua.
Cultivos discontinuos o por lotes.
Es la forma de cultivar más evidente y es la que hemos estado asumiendo cuando en el tema anterior hemos definido los parámetros de crecimiento: se llena un recipiente con medio de cultivo, se inocula con una concentración inicial de biomasa Cb0 y se deja crecer. Una vez que se detiene el crecimiento (o cuando vd, el ingeniero decida) se abre el recipiente y se "cosecha" la biomasa.
En estas condiciones, un cultivo pasa por las siguientes fases:
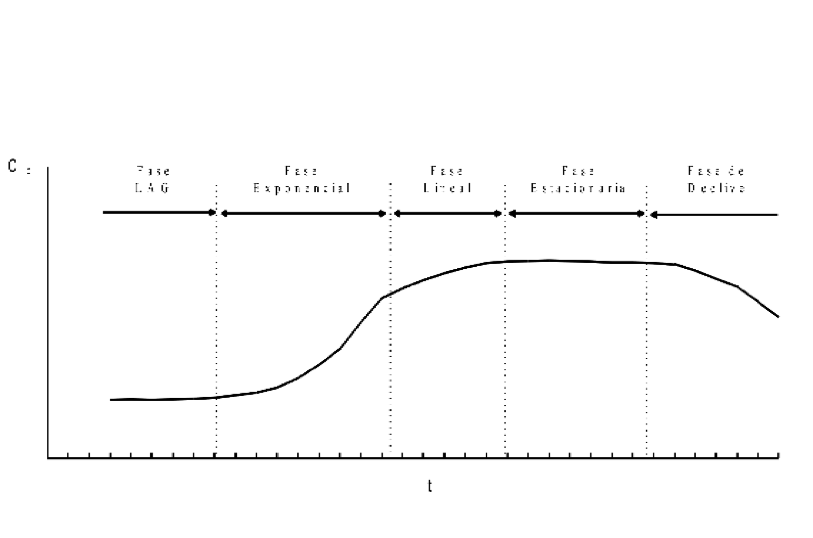
Las fases son las siguientes:
- Lag : fase inicial de crecimiento lento o nulo que tiene lugar mientras los organismos se acostumbran al nuevo entorno. Puede no existir
- Exponencial : fase de crecimiento a la máxima velocidad específica. Es posible al no haber limitación de nutrientes
- Lineal (ralentización) : tiene lugar cuando aparece un nutriente que lelga a ser limitante. Si el nutriente limitanse llega en forma continua (como pasa con la luz e microalgas) se observa una fase lineal.
- Estacionaria : las condiciones se vuelven tan limitantes que µ baja hasta que µbruta=m y por tanto µneta=0.
- Declive : comienza a haber muerte celular a un rirmo significativo. Se puede describir una µmuerte aunque nosotros no lo hacemos porque esta fase no nos interesa.
Además de fases intermedias que a veces se confunden con las que acabamos de describir.
Pero lo importante es lo que µ no es constante, si no que varía con las condiciones del cultivo y lo que es más importante desde el punto de vista del ingeniero: µ llega a hacerse cero y con ello Pb también se hace cero, por lo que no interesa seguir manteniendo el cultivo.
De hecho, como demostraremos, no interesa mantener al cultivo hasta la fase estacionaria ya que durante la transición de la fase lineal a la estracionaria, la Pb instantanea va disminuyendo y llega a hacer disminuir la Pb media.
BALANCE DE MATERIA DIFERENCIAL EN CULTIVOS POR LOTES
El balance de materia diferencial permite obtener la concentración de biomasa Cb y la productividad Pb instantaneas en función del tiempo. Es la ecuación de diseño de un FBR en discontinuo ya que la variable de diseño con la que podemos jugar es el tiempo de cultivo. La ecuación general de balance de materia que aplicamos es:
[Entrada]+[Generación]=[Salida]+[Consumo]+[Acumulación]
Puesto que en un cultivo por lotes no hay entrada ni salida durante la operación, se cumple:
BALANCE DE MATERIA INTEGRADO (O DISCRETO) EN CULTIVOS POR LOTES
El balance de materia integrado sirve para conocer µ y Pb en funcion de t, permitiendo predecirlo y así optimizar el fotobiorreactor sobre el papel. Cuando µ es constante, la ecuación que da Cb(t) es la conocida ecuación exponencial. Sin embargo, en sino que es:
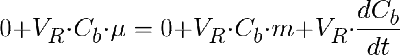
Recordemos que VR es el volumen del dispositivo de cultivo. Simplificando y reodenando, queda
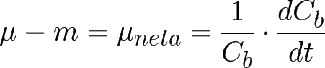
Ecuación que ya ha visto vd. antes porque es la definición de velocidad específica de crecimiento pero escrita de manera más formal. Esta ecuación no le sirve para predecir nada, pero si que sive para obtener µ a partir de datos experimentales de Cb frente al tiempo y disponer de datos de µ vs. t y de datos de µ vs Cb que nos servirán para obtener modelos de crecimiento en el Tema 3.
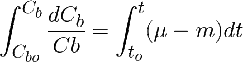
Que queda:
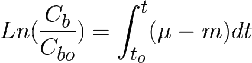
Para obtener Cb(t) hay que conocer la relación entre µ y t o, la relación entre µ y Cb.
Más interés tiene la expresión de la productividad volumétrica media obtenida como ∆Cb/∆t en un intervalo discreto de tiempo [to, tf]:
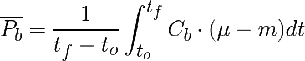
Donde ts es el tiempo de servicio entre lotes. este es el tiempo que se necesita para limpiar, rellenar y reinocular. La ecuación es difícil de usar porque se necesita un modelo de crecimiento y se ha de integrar conjuntamente con Cb(t). Sin embargo, lo importante es el concepto: en un cultivo batch la productividad volumétrica de la operación (promedio fernte a la instantánea) se puede maximizar esogiendo la concentración inicial y el tiempo óptimo de operación.
Esto se puede analizar numéricamente con una tabla del tipo:
Realizaremos un ejemplo en clase.
Puede bajar los datos de Cb frente al tiempo aquí.
Cultivos continuos
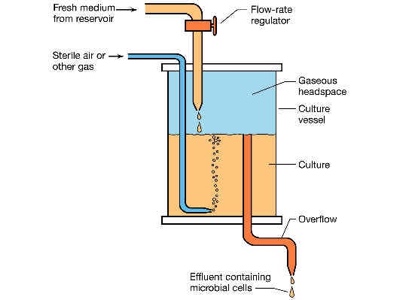
En un cultivo continuo se está introduciendo medio constantemente a una tasa constante. El volumen de cultivo se mantiene constante por medio de un rebosadero. Esto es un cultivo en continuo a volumen constante. Otras configuraciones son posibles, pero esta es la que vamos a utilizar nosotros.
BALANCE DE MATERIA DIFERENCIAL EN CULTIVOS CONTINUOS
Usamos la misma ecuación general de balance que en el caso anterior. Ahora sí existen términos de entrada y salida aunque si usamos para diluir medio fresco exento de biomasa, la entrada de biomasa es nula (podría ser medio recirculado).
[Entrada]+[Generación]=[Salida]+[Consumo]+[Acumulación]
Llamando Q al caudal volumétrico de adición de medio fresco, la ecuación queda:
o, mejor:
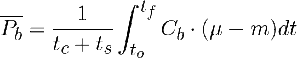

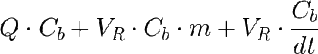
Cbi es la concentración en el medio fresco y por tanto igual a cero para nosotros. Reagrupando µ y m y reordenando, queda:
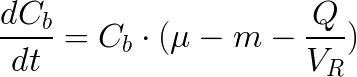
Que es la ecuación diferencial que permite conocer Cb(t) en un cultivo en continuo. Al cociente Q/VR se le denomina "velocidad de dilución" y se le representa por la letra D.
BALANCE DE MATERIA INTEGRADO EN CULTIVOS CONTINUOS
El caso general es demasiado complicado para un curso de introducción y, además, solo es útil en aplicaciones especializadas (como el control de procesos). Sin embargo existe un caso que es muy habitual y muy util: el ESTADO ESTACIONARIO.
- Estado estacionario : Conforme Cb se incrementa desde el inicio del cultivo, la salida va haceindose más grande hata que llega a igualar a la generación. En este caso, el térmico dCb/dt se hace nulo.
La ecuación que rige este caso es:
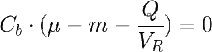
Fácil ¿verdad?. Esto significa que en un cultivo en continuo se puede imponer la µneta imponiendo D, es decir, el caudal de refresco Q. Por eso los cultivos continuos son tan fáciles de analizar. Además, la productividad es muy facil de obtener ya que Pb=Cb·D. Sin embargo, para poder calcular Pb una vez impuesta D, necesitamos Cb y para calcular Cb necesitamos el modelo de crecimiento que veremos en el Tema 3.
Cultivos semicontinuos
El problema de los cultivos continuos es que no es siempre posible estar diluyendo y cosachando. Por ejemplo, en cultivos que usan luz solar, no es conveniente diluir por la noche. O no es conveniente cosechar si no se puede centrifugar. Una solución intermedia son los cultivos semicontiuos: se operan de forma similar a los batch, pero sólo se cosechan parcialmente a intervalos regulares, reponiendo el cosechado con medio fresco.
Es como repetir un cultivo batch indefinidamente, con la ventaja añadida de que nos ahorramos la mayor parte del tiempo de servicio entre lotes ts.
Las ecuaciones que rigen el sistema son las mismas que en el caso discontinuo. Maximizar la productividad pasa por decidir el nivel de dilución (fracción renovada) y el tiempo de cultivo, que es lo mismo que decidir Cbo al principio de cada ciclo y Cbf al final de la misma forma que en un sistema discontunuo.
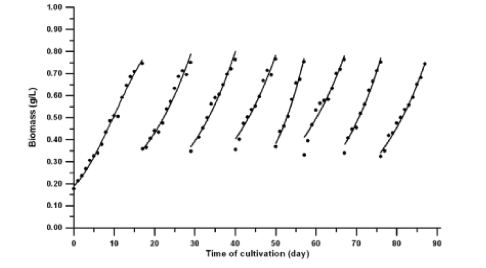
Cultivo semicontinuo de Spirulina platensis.
El ciclo de cosechado y dilución se repite una y otra y otra y otra vez.
Cuestiones
1 - ¿En qué fase es más alta la velocidad específica de crecimiento en un cultivo por lotes?
2 - ¿Coincide la máxima velocidad de crecimiento y la máxima productividad volumétrica en un cultivo por lotes? ¿Por qué?
3 - En un cultivo continuo, ¿qué ocurre si se fija una D superior a la µmax?
4 - Un cultivo continuo se encuentra en estado estacionario a, por ejemplo, D=µmax/2 ¿Qué odurre si se disminuye D? ¿Y si se aumenta D sin que suepere µmax?.
5 - ¿Es posible un estado estacionario en un cultivo discontinuo? ¿En qué se diferencian la fase estacionaria y el estado estacionario?
1.5 - Cultivos por lotes, continuos y semicontinuos
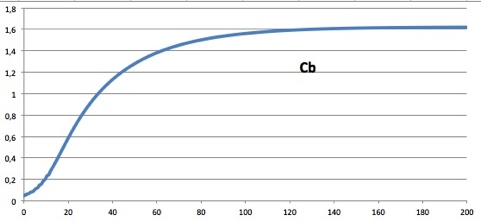
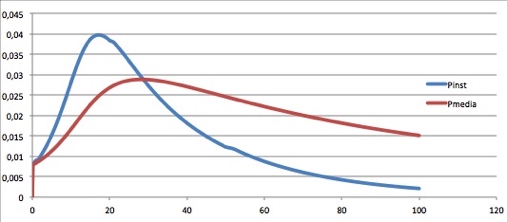
Cb (g/L)
tiempo (h)
tiempo (h)
P instantanea y media
(g/L/h)
Ejemplo de cultivo en batch.
Se muestra la evolución de la concentración de biomasa hasta la fase estacionaria y las productividades instantaneas y media del ciclo.
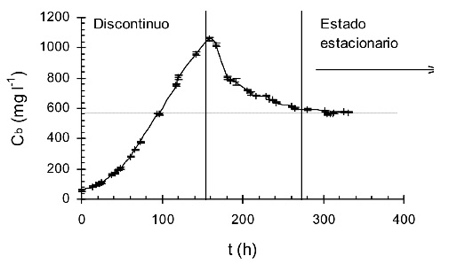
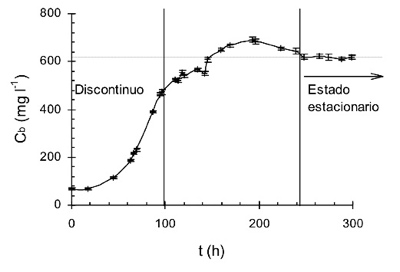
Ejemplo de cultivos en continuo.
Cultivos de Isochrysis galbana llegando al estado estacionario.