Ingenieria de Procesos aplicada a la Biotecnología de Microalgas

3.6 - Optimización de cultivos en continuo.

Por fin tenemos todos los elementos necesarios para optimizar la productividad de un FBR. Estos elementos son:

          ● El modelo de disponibilidad de luz (Iav en función de Cb, ka y la geometría del FBR).

          ● El modelo de crecimiento (µ en fución de Iav).

          ● El balance de materia del caso (cultivo discontinuo, continuo, estado estacionario ...etc)

Apliquemos el procedimiento a un caso concreto que es la mejor forma de aprenderlo.

DISPONIBILIDAD DE LUZ

Es un caso bastante claro: geometría plana e incidencia perpendicular. La ecuación que da la disponibilidad de luz es:

Ecuaciones

Vamos a optimizar un fotobiorreactor que va a funcionar en continuo y en estado estacionario. Asumimos buena mezcla (integración de irradiancias) e iluminación exterior constante.

El ejemplo es un fotobiorreactor plano de 5 cm de espesor y 500 L de volumen útil que se encuentra iluminado por 1500 mE m-2s-1 que incide perpendicularmente sobre el FBR.

Las propiedades ópticas de la biomasa son constantes y vienen definidas por ka=0,19 m2g-1.

Como modelo de crecimiento vamos a usar el de Camacho-Rubio con los parámetros µmax=0,045 h-1, α=180 µE m-2s-1, κ=0,075 y m=0,005 h-1.

Veamos las ecuaciones que rigen el ejemplo.

Definición del ejemplo

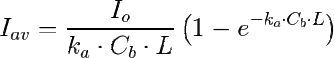
que con ka=0,19 m2g-1, Io=1500 mE m-2s-1 y L=0,05 m, queda:

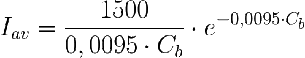
MODELO DE CRECIMIENTO

Vamos a usar el modelo de Camacho-Rubio. La ecuación es:

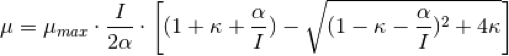
que con los parámetros µmax=0,045 h-1, α=180 µE m-2s-1y κ=0,075, y la condición de intefración de irradiancias, queda:

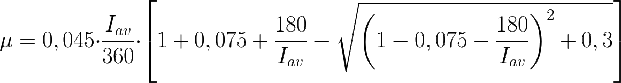
BALANCE DE MATERIA

El balance de materia es el caso del cultivo en continuo en estado estacionario:

Para este caso, lo despejamos como:

Ecuacion 1

Ecuacion 2

Ecuacion 3

Las 3 ecuaciones que hemos escrito nos permiten realizar la siguiente secuencia de cálculos que simularía la operación del FBR:

          ● Imponer D.

          ● Calcular µ con la ecuación 3.

          ● Calcular la Iav necesaria para esa µ con la ecuación 2

          ● Calcular la Cb correspondiente a la Iav con la ecuación 1

          ● Calcular Pb como D·Cb.

          ● Repetir hasta obtener el valor de Pb máximo posible

Pero este esquema de cálculo que es el mas directo y natural requiere resolver implicitamente las ecuaciones 1 y 2, lo que es un engorro y hace el proceso largo y trabajoso. Es mucho mejor hacer lo siguiente que da el mismo resultado:

          ● Imponer Cb.

          ● Calcular Iav con la ecuación 1.

          ● Calcular µ con la ecuación 2

          ● Calcular la D correspondiente al estado estacionario con la ecuación 3

          ● Calcular Pb como D·Cb.

          ● Repetir hasta obtener el valor de Pb máximo posible

Mucho más rápido e inmediato, como se muestra en la siguiente hoja de cálculo:

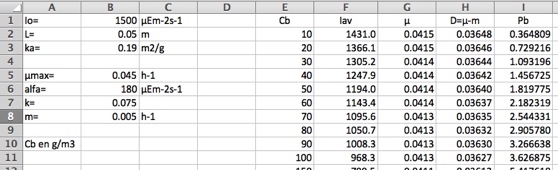
Optimización

Máximo

Compensación

Tabla de optimización

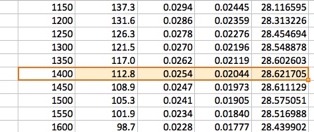
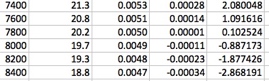
La tabla muestra que a D=0.0202 h-1 se establece un estado estacionario con concentración de biomasa Cb=1400 g m-3 que da una productividad de biomasa Pb=28,62 g m-3 h-1.

Si lo desea, puede afinar más iterando cn más finura en concentraciones de biomasa entre 1300 y 1500 g m-3, que es donde está el máximo.

Con esta solución, y puesto que el volumen del FBR es de VR=500 L, el caudal de medio entrante ha de ser Qv=VR·D=10,22 L h-1.

Usando los coeficientes obtenidos en el apartado 1-6:

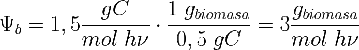
Obtenemos que el FBR está fijando FT=Pb/Ψb =9,54 mol de fotones por hora.

Puesto que el reactor tiene 500 L y 5 cm de espesor y siendo VR=S·L, la sección que intercepta el FBR es S=0,5(m3)/0,05(m)=10 m2. Por tanto, estaría interceptando 1500(µ Em-2s-1)·10(m2)·3600(s h-1)=54 moles de fotones por hora.

Lo que es un rendimiento como del 17%, que probablemente está un poco sobreestimado porque no toda la raciación que incide se absorbe.

Si calcula el flujo total absorbido como FT=Iav·Cb·ka·VR obtendrá un resultado más ajustado.

La gráfica muestra que la elección de D no es crítica, ya que la zona de máximo es bastante plana. De hecho, si hace un análisis económico es posible que le interese oerder un poco de productividad a cambio de reducir el gasto en medio (agua que no nutrientes), operando a D=0,15 o incluso a D=0,012 h-1.

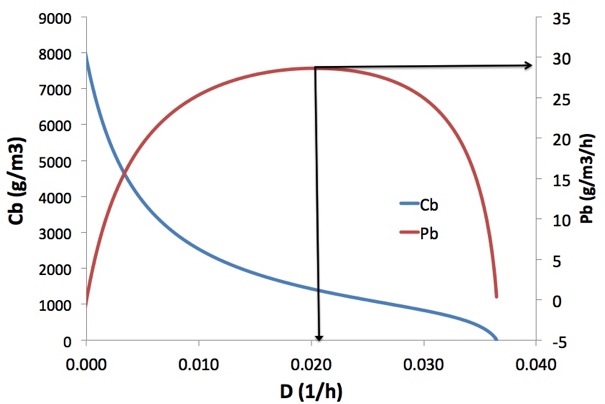
Este resultado se muestra de una forma más intuitiva con la siguiente gráfica:

Usando los coeficientes del apartado 1-6 se puede completar el problema calculando que la generación de oxígeno del sistema en el óptimo encontrado será de unos 38 g por hora o lo que es lo mismo 1,19 moles o 26,7 L c.n.

Y necesitará 47,7 g de CO2 por hora.

Se puede también calcular la cantidad necesaria de nitrato sódico en el medio fresco suponiendo que la biomasa contene un 5% de N. Esto lo dejamos para clase.

Como ve, este análisis deja el diseño básico muy avanzado y permite estudiar muchas posibilidades de la operación.

3.6 - Optimización de cultivos en continuo

Cuestiones

1 - Complete los cálculos de consumo de N y calcule la concentración de nutrientes en el medio si el N se suministrase como cloruro amónico. A decir verdad, debería revisarlo todo para asegurarse de que no me he equivocado.

2 - Repita los cáculos con D=0,012.

3 - ¿Qué pasaría si este FBR estuviese iluminado por el sol e Io cambiase hora a hora?

Si le interea, puede ver aquí un ejemplo en MathCad correspondiente a un FBR cilindrico trata do rigurosamente con el modelo de Evers.