Ingenieria de Procesos aplicada a la Biotecnología de Microalgas
2.2 - Cálculo del coeficiente de extinción en cultivos de microalgas.
La ecuación de la atenuación exponencial de la luz, que podriamos llamar ecualcin de Lambert-Beer, puede despejarse de la siguiente manera para un dispositivo de paso óptico conocido L:
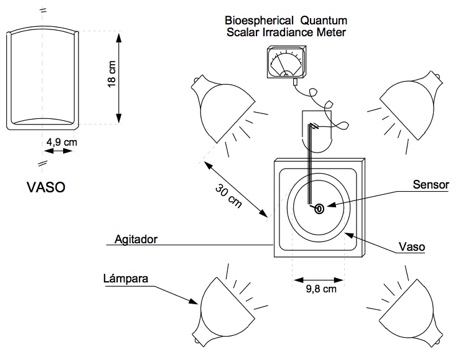
Medida del ka de un cultivo de microalgas
Lo que significa que la representacion de Ln(Io/I) frente la concentración de biomasa Cb produce una linea recta de pendiente kaλ·L. Llamemos m a esta pendiente.
He usado el subindice λ para simbolizar que en principio esta ecuación sólo es cierta para una longitud de onda determinada. De otra forma, en rigor, ka no sería una constante y no podría salir de la integral ∫ka·dx.
El dispositivo de medida puede ser una cubeta de un espectrofotómetro o un motaje como el mostrado en el esquema de al lado. Dese cuenta de que lo importante es que el sensor está situado en el cento del vaso cilíndrico, de forma que los haces de luz viajan una distancia R a traves del cultivo antes de alcanzar el sensor.
De esta forma, es posible realizar experimentos en los que se mide I en función de la concentración de biomasa, como los que se muestran en la tabla de debajo.
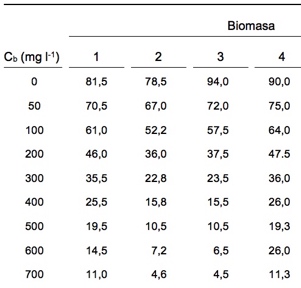

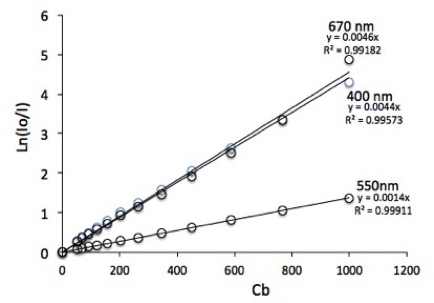
Representando Ln(Io/I) se obtiene una linea que es recta en el tramo en el que se cumple la ley de Lmbert-Beer. En ese caso, se cumple que la pendiente de esa linea, m, es:
Y, por tanto, se puede despejar el coeficiente de extinción como:
En el caso del cilindro:
Como puede ver en la gráfica de la derecha, la ley de Lambert-Beer se cumple bastante bien incluso a concentraciones relativamente altas y los coeficientes de extinción pueden variar considerablmente con la longitud de onda.
La gráfica de la derecha muestra casos extremos ya que se han elegido longitudes de onda muy bien absorbidas y la de 550 nm que es la peor absorbida por la clorofila y que es la razón que le da a las plantas y a muchas microalgas su color verde.
La gráfica de la derecha muestra datos de Muriellopsis sp. en una cubeta de 1 cm de paso (L=0,01 m).
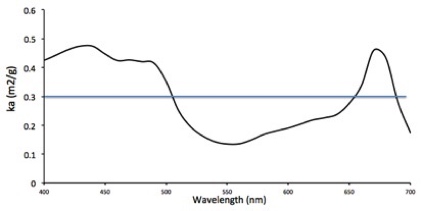
En la gráfica de debajo puede vd ver los valores de kaλ en todo el espectro PAR.
Gráfica 2
Estrictamente hablando, vd puede calcular kaλ con una sola medida de I a un valor único de Cb según:
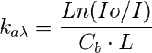
Sin embargo es poco riguroso ya que no asegura que se cumpla la ley de Lambert-Beer en el intervalo y está sujeto a error de magnitud indeterminada.
Esto es lo que hace mi calculadora de ka monopunto. Puede usarla como demostración aquí.
Pese a que la ley de Lambert-Beer es rigurosa a una longitud de onda, se ha demostrado experimentalmente que se puede usar con luz policromática (blanca) en microalgas con cierta precisión. También se ha demostrado teóricamente y se han acotado las condicones en las que esto sucede, pero no lo abordaremos en este curso.
Debajo se muestran experimentos de medida de absorbancia de Isochrisis galbana en un cilindro. Como se puede comprobar, la ley de Lambert-Beer se cumple satisfactoriamente.
ka en luz policromática: ka medio
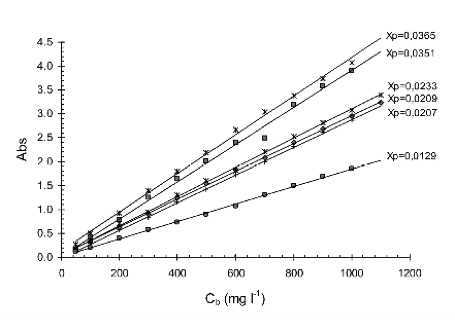

Otra cosa importante que muestra la gráfica de arriba (gráfica 2) es que ka puede depender del contenido en pigmentos de una forma bastante significativa. Si el contenido en pigmentos de su microalga se modifica, debería considerar medir el ka en varias circusntancias y encontrar una relación entre ka y el contenido en pigmentos.
La gráfica de la derecha muestra ka como una función lineal del contenido en pigmentos expresado como fracción másica.
Naturalmente, a mayor contenido en pigmentos más alto es el valor de ka que cabe esperar.
ka es función del contenido en pigmentos.
Este ka obtenido con luz blanca es un promedio del correspondiente a todas las longitudes de onda QUE DENOMINAREMOS ka MEDIO y DEPENDE de la COMPOSICIÓN CROMÁTICA de la luz. Es decir, en principio puede ser diferente medido con luz del Sol, fluorescente o incandescente. Incluso puede variar de la mañana a la noche ya que el color de la luz del ol varía a lo largo del dia.
Por supuesto, al ser una observación experimental, la validez del presupuesto debe ser comprobada para cada microalga y, lo que es más importante : debe ser medido con la luz que se vaya a utilizar para la iluminación
Gráfica 3

Cuestiones
1 - ¿Qué significado tienen las unidades del ka?
2 - ¿Cómo influyen las unidades en las que se expresa I al medir el ka? ¿Es igual usar µE m-2 s-1 que quanta cm-2 s-1?
3 - ¿Importa en qué unidades se ponga el camino óptico L para calcular ka?
4 - ¿Qué consecuencias tendría que el el experimento mostrado en la Grafica 1 el sensor no estuviese en el centro?
5 - En el experimento de medida del ka mostrado en la gráfica 1 ¿importa el tamaño del sensor?
6 - Calcule ka para los datos mostrados en la gráfica 2. Recuerde que se han realizado en una cubeta de espectrofotómetro de L=1 cm.
2.2 - Cálculo del coeficiente de extinción en cultivos de microalgas.
Gráfica 1
