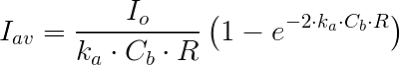Ingenieria de Procesos aplicada a la Biotecnología de Microalgas
Los cálculos del capítulo anterior demuestran que en el seno de los cultivos de microalgas existen amplias zonas oscuras que coexisten con partes intensamente iluminadas.
¿Cómo definir un número que de una medida fiable de la iluminación en un cultivo denso? Tal número debe ser una media que tenga en cuenta la existencia de zonas iluminadas y oscuras, dándo más pesoa los valores de irrdiancia según la extensión que ocupen.
Este número es una media ponderada al volumen.
2.4 - Irradiancia promedio en sistemas planos y cilíndricos.
Si tenemos un cultivo constituido por dos volumennes V1 y V2 iluminados con I1 e I2 respectivamente, podemos definir la media volumétrica:
Irradiancia promedio.
Que se puede definir para un número indefinido de elementos:
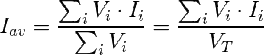
Donde VT es el volumen total de cultivo. Para una distribución continua de I tal como las que hemos estado viendo y que en general es I(x,y,z), Vi es un diferenciad de volumen dV y la suma es una integral:
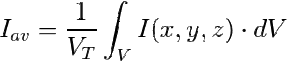
A continuación utilizaremos las expresiones de distribución de irradiancia en los diferentes sistemas estudiados en el epígrafe anterior para encontrar fórmulas que dan la Iav en diversos sitemas de interés. El truco para poder integrar las expresiones consiste en escribir el diferencial de volumen de la forma más fácil posible.
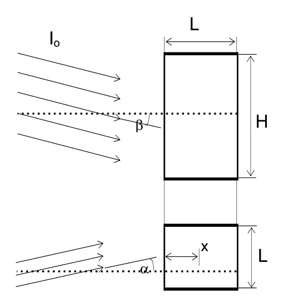
Flujo directo perpendicular
Recordamos que la función de distribución es:
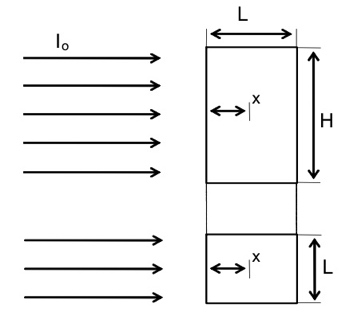
Geometría plana, flujo directo.
El diferencial de volumen se escribe fácilmente teniendo en cuenta que I solo varia en el sentido de las x (de 0 a L) y no en el sentido de altura (z, que varia de 0 a H) ni la anchura (y, que varia de 0 a A). Entonces
Donde S es H·A que es el area de la cara donde incide I. Entonces la irradiancia promedio puede escribrirse como:
Flujo directo inclinado
Basta usar la disribución correspondiente al caso. El diferencial de volumen es el mismo. Con el mismo razonamiento que en el caso anterior, se llega a la exptesión:
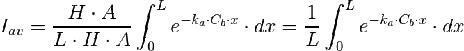
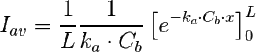
Que finalmente queda:
Ecuación fácil de aplicar y que indica que la única dimension que influye en la disponibilidad de luz es el espesor (anchura del reactor plano o profundidad de Receway).
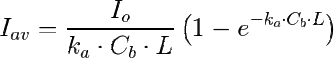
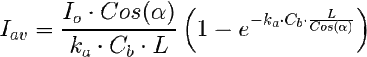
Flujo difuso en geometría plana
Hay que introducir la distribución del caso, vista en el epígrafe enterior, en la ecuación del promedio volumétrico (Ecuacion (1) mostrada arriba). Queda una entidad bastante complicada que no voy a poner porque de todas formas no lo vamos a usar en este tema.
La realidad es que las ecuaciones de la geometría plana (ecuaciones (2) y (3)) funcionan bastante bien bajo luz solar en atmósfera medianamente clara porque aunque hay una componente importante de difusa, ésta llega mayoritariamente de direcciones próximas a la principal (desde ø pequeños, es decir, poco desviada de la dirección de incidencia principal α).
Ecuacion (1)
Ecuacion (2)
Ecuacion (3)
Flujo directo y difuso
Por motivos de geometría que se discuten en Molina y cols. (1997) (separata 2 de los materiales proporcionados en este curso) en la geometria cilíndrica, Iav sale lo mismo para la distribución difusa que para la directa. CUIDADO: Iav sale lo mismo pero las distribuciones son diferentes.
Geometría cilindrica.
Curiosamente, por la geometría de la distribución difusa en el cilindro, el diverencial de volumen se escribe con más sencillez para la distribución difusa en coordenadas cilíndicas. Para un cilindro de radio R y altura H:
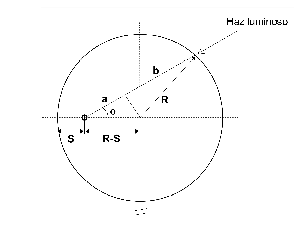
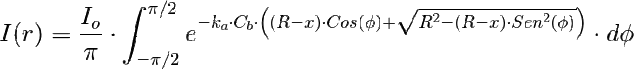
Entonces, es cuestión de meter la distribución de irradiancias del caso:
En la ecuación del promedio volumétrico adaptada al caso:
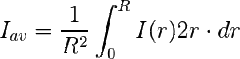
Ecuación que ha de ser evaluada numéricamente hunto con la del perfil. Venemos en un ejemplo de clase que es perfectamente realizable.
Geometria cilíndrica: ecuación simplificada
Se mire como se mire, usar la Ecuación (4) es un engorro. En un estudio numérico, Molina y colaboradores (1997) demostraron que es posible obtener Iav en un sistema cilíndrico en funcion de Cb y ka usando la ecuación (1) puesta de la forma:
Donde Leq es la longitud óptica equivamente del sistema que es función del radio y en las condicones más habituales vale Leq=1,60R, donde R es el radio del cilindro objeto de estudio. Leq varía entre 1,57R y 1,71R en condiciones extremas, aunque el intervalo en condicones de cultivo realistas se encuentra entre 1,57R y 1,63R, por lo que no se comete un error excesivo tomando Leq=1,6R como aproximación.
Ecuacion (4)
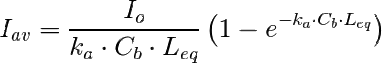

Puede afinar el cálculo en condiciones concretas usando la table que se muestra a la derecha para calcular Leq en función del ka, normalmente conocido, y la concentración de biomasa esperada.
En la practica, esta va a ser la ecuación que usemos siempres para calcular Iav en sistemas cilíndricos ya que da resultados prácticamente iguales a le Ecuación (4). Cuidado, porque esto funciona para la Iav (irradiancia promedio, una medida de la disponibilidad de luz) pero NO FUNCIONA PARA LA DISTRIBUCIÓN DE LUZ, que es muy diferente en sitemas cilíndricos y planos y también difiere mucho del caso de iluminación directa a difusa.
Cuestiones
1 - Calcule la disponibilidad de luz en una fotobiorreactor plano de L= 12 cm lleno de un cultivo de Cb=1,5 g/L (ka=0,25 m2/g) iluminada perpendicularmente por irradiancia directa de Io=800 µE m-2 s-1.
2 - Repita la cuestión anterior para una irradiancia incidente de Io=1200 µE m-2 s-1 que incide con un ángulo de 25º desviado de la perpendicular.
3 - Calcule la irradiancia promedio en una columna iluminada con irradiancia directa de Io=1000 µE m-2 s-1 sabiendo que contiene un cultivo de Cb=1,8 g/L con ka=0,2 m2/g.
4 - ¿Que ecuación usaría en un Raceway operando en el exterior en Almería? ¿Y en un fotobiorreator tubular operando dentro de un invernadero?.
2.4 - Irradiancia promedio en sistemas planos y cilíndricos
REFERENCIAS
Molina Grima et al (1997) Enzyme & Microbial Technology.
Molina Grima et al (1994) Journal of Biotechnology.
Flujo cilíndrico radial
Como ya dijimos, el caso es poco usual. Sin embargo, como tenemos la distribución:
la podemos integrar con el dV pertinente:
Y queda como resultado una función similar a la de la geometría plana, como puede vd comprobar: