Ingenieria de Procesos aplicada a la Biotecnología de Microalgas

La concentración de biomasa no es,  pues, una buena variable para correlacionar con µ en us sistema limitado por luz. Ya sabemos que la disponibilidad de luz viene dada por

          - Io

          - Cb

          - ka,

          - dimensiones y geometría del FBR.

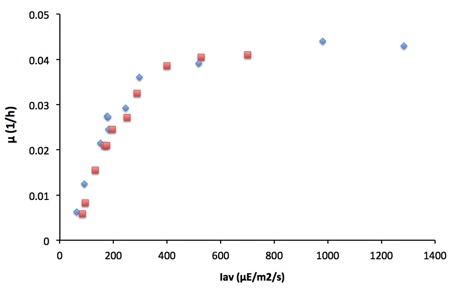
Representando µ frente a la disponibilidad de luz, como se muestra en la gráfica 2, está claro que existe una correspondencia entre µ e Iav.

El modelo de crecimiento es una ecuación que de esta relación entre µ e Iav. Esta ecuación es muy importante para nosotros ya que es la piedra de toque en el diseño y operación de FBRs.

Esta ecuación la denotamos como:

3.1 - Relación entre velocidad especifica de crecimiento y disponibilidad de luz: modelo de crecimiento

Conforme la concentración de biomasa aumenta, el cultivo se hace cada vez más opaco y la luz pennetra menos en su interior, produciendo zonas oscuras. Es esta situación de limitación por luz, es lógico que la velocidad específica de crecimiento disminuya.

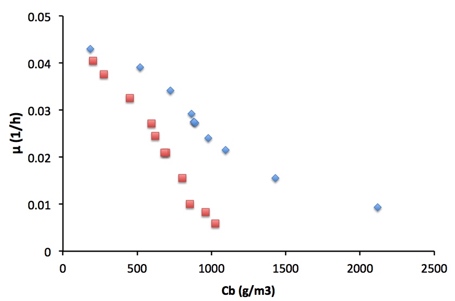
Tal y como se muestra en la gráfica de la derecha, un incremento en Cb provoca un descenso en µ. Sin embargo en la gráfica también se puestra que Cb no es un buen indicador de la disponibilidad de luz ya que a diferentes Cb pueden corresponder velocidades de crecimiento muy distintas.

En el ejemplo de la derecha se muestran datos de experimentos realizados en una columna de burbujeo agitada de unos 20 cm de radio. La diferencia entre los puntos rojos y azules es que ambas series han sido realizadas con diferente iluminación exterior, 900 y 1800 µEm-2s-1 respectivamente. La mayor disponibilidad de luz hace posible que la velocidad específica de crecimiento se mantenga a concentraciones de biomasa mayores.

Cuando la Cb se incrementa, µ disminuye

Io=1800 µEm-2s-1

Io=900

Gráfica 1

Gráfica 2

En los epígrafes siguientes estaremos viendo ecuaciones que nos sirven para correlacionar  estos datos. Pero antes tenemos que hacer una puntualizaciones para poder escoger una ecuación adecuada

Relación µ - Iav.

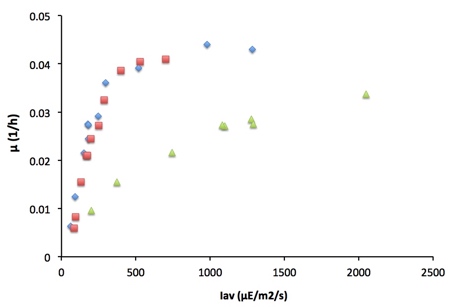
Gráfica 3

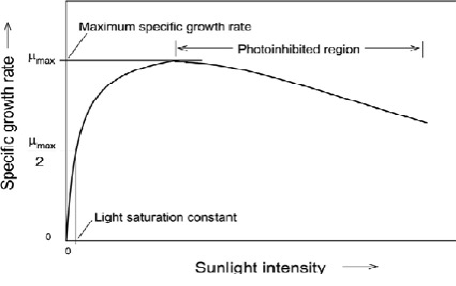
La relación unívoca entre velocidad específica de crecimiento e irradiancia promedio deja de cumplirse en ciertas ocasiones. Una de ellas es cuando existe fotoinhibición.

La fotoinhibición es una desactivación parcial reversible del sistema fotosintético que hace que la luz se aproveche menos. Tal y como se muestra en la gráfica de la derecha, gráfica 3, en condiciones de fotoinhibición en un cultivo denso se necesita una mayour iluminación para producir la misma µ.

Esto es así porque parte del aparato fotosintético está desactivado y parte de la luz que se absorbe no llega al metabolismo. La extensión de la fotoinhibición viene dada por un equilibrio entre la velocidad de desactivación y la de regeneración (es reversible):

Fotoinhibición.

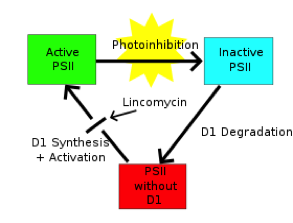
veremos modelos que incluyen fotoinhibición en epígrafes porteriores, con el objeto de saber tenerla en cuenta.

Sin embargo, el diseño correcto de FBRs pasa por EVITAR LA FOTOINHIBICIÓN, ya que esta es siempre una situación indeseable y evitable con unas condiciones de operación adecuadas. Es incluso preferible sombrear el FBR y que le llegue menos luz antes que dejar que se establezcan condiciones de fotoinhibición.

Dependiendo de la intensidad de la mezcla, pueden darse dos situaciones extremas respecto de la velocidad específica media observada en un cultivo:

        1  - En ausencia de agitación, las microalgas están cada una en un punto determinado del cultivo, (x,y,z), sometidas a la irradiancia local I(x,y,z). En este caso, las microalgas se aclimatarían a una irradiancia local y habria una distribución de velocidades de crecimiento, µ(x,y,z). La velocidad específica media observada sería un promedio volumétrico Llamamos a esta situación "integración de velocidades locales":

Importancia de la agitación y mezcla.

        2  - En presencia de agitación suficiente, las microalgas se mueven entre zonas oscuras e iluminadas lo suficientemente rápido como para aclimatarse a la irradiancia promedio Iav. En este caso, todas las microalgas "ven" Iav y la velocidad específica media observada sería función de la irradiancia promedio. Llamamos a esta situación "integración de irradiancia" que se define con la siguiente ecuación:

Por supuesto que cualquier situación intermedia entre las anteriores es posible.

La segunda situación siempre es mejor por varios motivos. Aparte de que la agitación es imprescindible, el principal motivo es que:

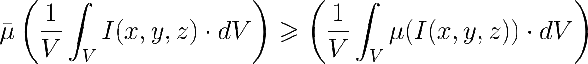
Es decir, que la situación de integración de irradiancias SIEMPRE da velocidades específicas de crecimiento mayores que la integración de velocidades locales.

El correcto diseño de FBRs pasa, por tanto, por proporcionar condiciones de agitación que permitan la situación de integración de irradiancias.

Se ha definido un número denominado FACTOR de INTEGRACIÓN que cuantifica si nos encontramos en una de las situaciones extremas o en alguna intermedia. El factor de integración:

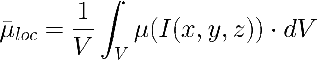
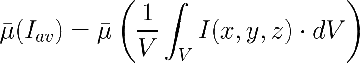
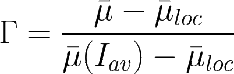
Que varía entre Γ=0 para la situación de integración de velocidades locales (µ=µloc) y la integración de irradiancia Γ=1 (µ=µ(Iav)).

La situaciones extremas pueden analizarse usando modelos estáticos, como veremos a continuación. Para analizar las situaciones intermedias se necesitan modelos dinámicos. En este curso fundamental nos centraremos en analizar situaciones de integración de irradiancias, aunque presentamos también los modelos dinámicos.

Veremos un ejemplo numérico de la diferencia entre esta dos situaciones al final del proximo apartado 3-5, cuando hayamos visto los modelos de crecimiento dinámicos y entendamos la importancia de la mezcla en cultivos densos.

3.1 - Relación entre velocidad específica de crecimiento y disponibilidad de luz

Cuestiones

1 - ¿Es preferible una situación de integración de luz o de integración de velocidades de crecimiento locales?

2 - ¿Qué quiere decir que Γ=0,5?

3 - ¿Qué pasa en el caso de la cuestión 2 si se aumenta la agitación?

4 - ¿Que pasa en el caso de la cuestión 2 si se incrementa la concentración de biomasa?