Próximo: El modelo de Cayley-Klein Arriba: La Geometría Proyectiva de Anterior: Acción de sobre el


Cónicas reales sobre el plano proyectivo real

En esta sección, emprendemos el estudio de las cónicas no degeneradas sobre $ \mathbb{R} P^2$. Nuestro objetivo es relacionar la aproximación algebraica de las secciones anteriores con la aproximación clásica de Chasles y Steiner.

El primer resultado importante sobre cónicas es que, salvo transformaciones proyectivas, son todas la misma. Con más precisión:

Ejercicio 4.1 (05)   Probar que si $ Q$ y $ Q'$son dos formas cuadráticas en $ \mathbb{R}^3$que definen dos cónicas no degeneradas (y no vacías) en $ \mathbb{R} P^2$, entonces existe una transformación lineal invertible $ M$ tal que $ Q'=Q\circ M$, o bien $ Q'=-Q\circ M$. Concluir que todas las cónicas no degeneradas sobre $ \mathbb{R} P^2$ son proyectivamente equivalentes.

Observación. De ahora en adelante todas las cónicas serán no degeneradas y no vacías.

Como consecuencia del ejercicio anterior, tenemos que es posible definir la razón doble de cuatro puntos sobre una cónica.

Ejercicio 4.2 (10)   Sean $ A,B,C,D$ cuatro puntos distintos sobre una cónica $ \mathcal C$. Si $ E$y $ F$son dos puntos sobre $ \mathcal C$diferentes de los anteriores, entonces las razones dobles $ [EA,EB,EC,ED]$ y $ [FA,FB,FC,FD]$ son iguales (Fig. 2). Usar esto para definir la razón doble de cuatro puntos sobre una cónica. Pista: considerar que $ \mathcal C$es una circunferencia y luego usar la conclusión del ejercicio 4.1 para reducir el problema a este caso.

 

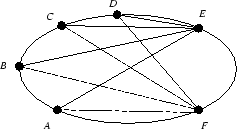
\epsfig {file=conic_ratio.eps}

f

Por dualidad, también podemos definir la razón doble de cuatro rectas tangentes a una cónica: sean $ a,b,c$ y $ d$ cuatro rectas tangentes a una cónica, sea $ e$ una quinta tangente a la misma cónica y definimos la razón doble $ [a,b,c,d]$ como la razón doble de los puntos $ e\cdot a, e\cdot b, e\cdot c$ y $ e\cdot d$ sobre la recta $ e$ (fig. 3)

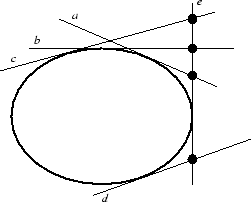
\epsfig {file=line_ratio.eps}

figura 3

Ejercicio 4.3   Sean $ X$e $ Y$dos puntos sobre una cónica $ \mathcal C$, podemos establecer una correspondencia entre el haz de rectas que pasan por $ X$y el haz de rectas que pasan por $ Y$: si $ l$ es una recta que pasa por $ X$, entonces corta a la cónica en algún otro punto $ Z$ o es la recta tangente a $ \mathcal C$que pasa por $ X$. En el primer caso, le asociamos la recta $ YZ$; en el segundo, la recta $ YX$ (fig 4). Usar el ejercicio 4.2 para probar que esta correspondencia conserva razones dobles y es, por lo tanto, una transformación proyectiva entre los haces.

 

\epsfig {file=line_correspondence.eps}

figura 4

 

Recíprocamente, tenemos la siguiente hermosa construcción de cónicas debida a Steiner.

Teorema 4.1   Sea $ f$ una transformación proyectiva entre el haz de rectas que pasan por un punto $ X$y el haz de rectas que pasan por un punto $ Y$. El conjunto

$\displaystyle C:=\{l\cdot f(l)\colon l\ $   es una recta que pasa por $\displaystyle X\} $

es una cónica.

Ejercicio 4.4 (10)   Probar que si la transformación proyectiva es una perspectividad, entonces la construcción da una cónica degenerada.

Si $ T$es una transformación proyectiva que lleva $ X$ a $ [0:1:0]$ e $ Y$a $ [1:0:0]$, entonces los haces de rectas que pasan por $ X$e $ Y$van a parar a los haces de rectas verticales y horizontales sobre el plano $ z=1$ (fig 5). Además, $ \mathcal C$se transforma en la gráfica de una función $ g$ del eje $ x$ al eje $ y$.

 

\epsfig {file=steiner.eps}

figura 5

Ejercicio 4.5 (10)   Usar que $ T\circ f\circ T^{-1}$ es una transformación proyectiva entre el haz de rectas que pasan por $ [0:1:0]$ (el haz de rectas verticales sobre el plano $ z=1$) y el haz de rectas que pasan por $ [1:0:0]$ (el haz de rectas horizontales), para probar que $ g$ es de la forma $ g(x)=(ax+b)/(cx+d)$. Concluir que $ T(\mathcal C)$es una hipérbola sobre el plano $ Z=1$ y utilizando esto demostrar el teorema 4.1.

Ejercicio 4.6 (10)   Enunciar el dual del teorema de Steiner. Este es el teorema de Chasles.

Usando el teorema de Steiner, fácilmente podemos demostrar que cinco puntos determinan una cónica. En efecto, sean $ A,B,C,D$ y $ E$cinco puntos sobre el plano. Si tres o más de estos puntos son colineales entonces es fácil ver que todos ellos están sobre una cónica degenerada. Supongamos ahora cualesquiera de estos tres puntos no son colineales. Observar que hay una única transformación proyectiva $ f$entre el haz de rectas que pasa por $ A$ y el haz de rectas que pasan por $ B$ tal que $ f(AC)=BC$, $ f(AD)=BD$ y $ f(AE)=BE$ (fig 6). Por el teorema de Steiner $ f$define una cónica que pasa por los cinco puntos.

 

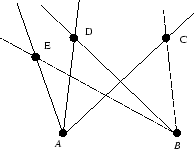
\epsfig {file=five_points.eps}

figura 6

Por la dualidad, tenemos que dadas cinco rectas, hay una única cónica que es tangente a todas ellas.

Como cinco puntos determinan una cónica, es claro que seis puntos no están sobre la misma cónica a no ser que satisfagan alguna condición especial. Esta condición, descubierta por el matemático y filósofo Blaise Pascal, es uno de los resultados más antiguos y bonitos de la geometría proyectiva.

Teorema 4.2 (Pascal)   Los seis vértices de un hexágono están sobre una cónica si y sólo si los tres puntos obtenidos al cortar los tres pares de lados enfrentados son colineales (fig 7).

 

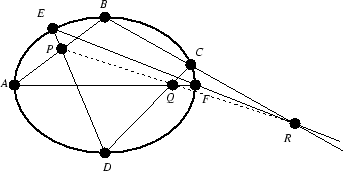
\epsfig {file=pascal.eps}

figura 7

Los dos ejercicios siguientes demuestran que si los seis vértices de un hexágono están sobre una cónica, los tres puntos obtenidos al cortar los tres pares de lados enfrentados son colineales. La demostración del recíproco utiliza las mismas ideas y se deja para el lector como un ejercicio menos estructurado.

Considerar la transformación $ f$que lleva los puntos de la recta $ ED$ a los puntos de la recta $ EF$definida mediante la siguiente construcción:

1.    Si $ X\in ED$, dibujamos la recta $ AX$.

2.    Sea $ A'$ el segundo punto de intersección de la recta $ AX$con la cónica.

3.    Dibujamos la recta $ CA'$.

4.    Sea $ Y:=f(X)$ el punto $ EF\cdot CA'$.

Ejercicio 4.7 (05)   Demostrar que la transformación $ f$es una perspectividad.

Ejercicio 4.8 (05)   Probar que $ f(P)=R$ y que el centro de perspectiva es $ Q$. Comprobar que con esto se demuestra la primera parte del teorema de Pascal.

Ejercicio 4.9 (10)   Probar que si los tres puntos obtenidos al cortar los tres pares de lados enfrentados de un hexágono son colineales, sus vértices quedan sobre una cónica.

El dual del teorema de Pascal es el siguiente resultado debido a Brianchon.

Teorema 4.3 (Brianchon)  Los seis lados de un hexágono son tangentes a una cónica si y sólo si las tres rectas obtenidas uniendo los tres pares de vértices enfrentados son concurrentes (fig 8).

\epsfig {file=brianchon.eps}

figura 8

Próximo: El modelo de Cayley-Klein Arriba: La Geometría Proyectiva de Anterior: Acción de sobre el

Versión Inglesa: Juan Carlos Alvarez 2000-10-27
Traducción: David Llena Carrasco 2003-06-25