Próximo: Motivación

La Geometría Proyectiva de las Cónicas

Juan Carlos Jimenez Paiva

Este capítulo está dedicado al estudio proyectivo de las cónicas. Comenzamos estudiando la acción del grupo lineal sobre el espacio de las formas cuadráticas. Después de probar que una cónica no degenerada sobre el plano proyectivo es equivalente a una circunferencia, mostramos que la razón doble de cuatro puntos sobre una cónica está bien definida, demostramos los teoremas de Chasles y Steiner que caracterizan las cónicas en término de transformaciones proyectivas, y probamos los teoremas de Pascal y Brianchon.

En la sección anterior, estudiamos la acción del subgrupo de transformaciones proyectivas que conservan una cónica dada $\mathcal C$, el exterior y el interior de $\mathcal C$. La acción sobre el interior es transitiva y conserva una métrica. Luego probamos que en esta métrica - el modelo de Cayley - Klein para la geometría hiperbólica - las geodésicas son las rectas.

Notas

• Todos los párrafos precedidos por un asterisco (*) se pueden dejar para una segunda lectura.
• Al lado de los ejercicios hay un número de dos dígitos entre paréntesis que describe su grado de dificultad. Los ejercicios más simples son calificados por (00), mientras que los más difíciles - los que podrían llevar una semana de intenso trabajo cerebral - tienen una valoración de (50).

 

• Motivación
• Conceptos algebraicos básicos
• Acción de 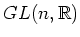$GL(n,\mathbb{R})$sobre el espacio de formas cuadráticas sobre $\mathbb{R}^n$
• Cónicas reales sobre el plano proyectivo real
• El modelo de Cayley-Klein para la geometría hiperbólica
• Sobre este documento ...

Próximo: Motivación