Próximo: Cónicas reales sobre el Arriba: La Geometría Proyectiva de Anterior: Conceptos algebraicos básicos

Acción de 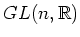$GL(n,\mathbb{R})$ sobre el espacio de formas cuadráticas sobre $\mathbb{R}^n$

Sea $A$ una matriz $n\times n$ simétrica y $Q(v):=v^tAv$ su forma cuadrática asociada. Si $M$ es una matriz $n\times n$ invertible, entonces $Q(Mv)=v^tM^tAMv$. Nótese que la función $v\mapsto Q(Mv)$ es una nueva forma cuadrática.

El objetivo de los siguientes ejercicios es estudiar la acción inducida del grupo general lineal sobre el espacio de formas cuadráticas.

Ejercicio 3.1 (05)   Probar que la aplicación $\mu(A,M):=M^tAM$ define una acción por la derecha de $GL(n,\mathbb{R})$sobre el espacio vectorial de las matrices $n\times n$ simétricas.

Ya que esta acción no es transitiva, estamos interesados en estudiar sus órbitas. En otras palabras, considerando dos matrices simétricas $A$ y $B$, deseamos determinar si existe una matriz invertible $M$ tal que $B=M^tAM$.

Definición 3.1   Sea $Q$ una forma cuadrática sobre $\mathbb{R}^n$. La nulidad de $Q$es la nulidad de su forma bilineal simétrica asociada. El índice de $Q$es $m$ si existe un subespacio $m$-dimensional $W$ tal que la restricción de $Q$a $W$ es definida negativa, y no existe ningún otro subespacio de dimensión mayor con esta propiedad.

Ejercicio 3.2 (05)   Sea $Q$una forma cuadrática sobre $\mathbb{R}^n$, sea $M$ una matriz $n\times n$invertible y sea $Q_M$la forma cuadrática $v\mapsto Q(Mv)$. Demostrar que la nulidad y el índice de $Q$ y de $Q_M$son iguales.

Ejercicio 3.3 (05)   Probar que si $A$ es una matriz $n\times n$ diagonal, entonces la nulidad de la forma cuadrática asociada es igual al número de ceros sobre la diagonal y el índice es igual al número de entradas negativas.

El resultado principal de esta sección es el siguiente teorema:

Teorema 3.2   Sean $Q$ y $Q'$dos formas cuadráticas sobre $\mathbb{R}^n$. Si la nulidad y el índice de $Q$ y de $Q'$son iguales, entonces existe una matriz invertible $M$ tal que $Q'(v)=Q(Mv)$para todo $v\in\mathbb{R}^n$.

En particular, el conjunto de las órbitas de la acción del grupo lineal general $GL(n,\mathbb{R})$ sobre el espacio de formas cuadráticas sobre $\mathbb{R}^n$está en correspondencia biunívoca con el conjunto de pares $(\nu,i)$, donde $\nu$ e $i$ son números enteros no negativos con $\nu+i<n$.

La prueba del teorema 3.2 es bastante simple, basta recordar algo de álgebra lineal.

Ejercicio 3.4 (-10)   Repasar los apuntes de álgebra lineal y recordar de nuevo el teorema (y su demostración) que asegura que si $A$ es una matriz $n\times n$ simétrica entonces existe una matriz ortogonal $R$ tal que $R^{-1}AR$ es diagonal.

Nótese que si $R$ es ortogonal, $R^{-1}=R^t$. Esto quiere decir que cada órbita contiene una matriz diagonal.

Ejercicio 3.5 (05)   Probar que si $D$ es una matriz diagonal, existe una matriz invertible $M$ tal que $M^tDM$ es diagonal y todas sus entradas son 1 o -1, o 0. Pista: $M$ se puede escoger diagonal.

Ejercicio 3.6 (05)   Sea $D$ una matriz $n\times n$ diagonal tal que $\nu$ es el número de entradas en la diagonal iguales a cero, $i$ es el número de entradas iguales a -1, y el resto son iguales a 1. Demostrar que existe una matriz invertible $P$ tal que $P^tDP$es un matriz diagonal cuyas primeras $n-i-\nu$ entradas diagonales son iguales a $1$, las $i$ entradas siguientes iguales a $-1$, y las $\nu$ últimas entradas iguales a cero. Pista: tomar $P$ como producto de matrices elementales.

Ejercicio 3.7 (05)   Probar que si $A$ es una matriz $n\times n$ simétrica cuya forma cuadrática asociada tiene nulidad $\nu$ e índice $i$, entonces existe una matriz invertible $M$ tal que $M^tAM$ es una matriz diagonal cuyas $n-i-\nu$ primeras entradas diagonales son iguales a $1$, las $i$ entradas siguientes iguales a $-1$, y las $\nu$ últimas entradas iguales a cero. Usar esto para demostrar el teorema 3.2.

Ahora aplicaremos las ideas precedentes al estudio de hipercuádricas proyectivas sobre $\mathbb{R}P^n$.

Ejercicio 3.8 (00)   Sea $Q$una forma cuadrática sobre $\mathbb{R}^{n+1}$ y sea $\mathcal Q\subset \mathbb{R}P^n$ la hipercuádrica proyectiva asociada. Si $M$ es una transformación lineal invertible de $\mathbb{R}^{n+1}$, la hipercuádrica asociada a la forma cuadrática $Q\circ M$ es la imagen de $\mathcal Q$ por la transformación proyectiva inducida por la inversa de $M$.

El ejercicio anterior nos dice que si $Q$ y $Q'$están en la misma órbita de la acción de $GL(n+1,\mathbb{R})$, entonces las hipercuádricas proyectivas que definen son proyectivamente equivalentes. El recíproco es casi cierto, pero no exactamente: las formas $x_1^2+x_2^2-x_3^2$ y $-x_1^2-x_2^2+x_3^2$ tienen índices diferentes, pero definen la misma cónica.

Ejercicio 3.9 (05)   Sean $Q$y $Q'$dos formas cuadráticas sobre $\mathbb{R}^{n+1}$ tal que sus hipercuádricas asociadas son proyectivamente equivalentes. Demostrar que la nulidad de $Q$ es igual a la nulidad de $Q'$y el índice de $Q$ es igual, o al índice de $Q'$, o a $n+1$menos el índice de $Q'$.

Ejercicio 3.10 (15)   Sea $Q$una forma cuadrática no degenerada sobre $\mathbb{R}^{n+1}$ y sea $\mathcal Q\subset \mathbb{R}P^n$ su hipercuádrica asociada. Relacionar el índice de $Q$ con el máximo de las dimensiones de todos los subespacios proyectivos contenidos en $\mathcal Q$.

Próximo: Cónicas reales sobre el Arriba: La Geometría Proyectiva de Anterior: Conceptos algebraicos básicos