Próximo: Conceptos algebraicos básicos Arriba: La Geometría Proyectiva de Anteior: La Geometría Proyectiva de

Motivación

Una sección cónica es, básicamente por definición, la imagen de una circunferencia bajo una perspectividad cuyo centro es el vértice del cono (fig. 1).

 

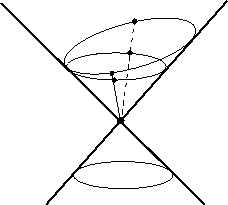
figura 1

Moviendo e inclinando el plano, podemos obtener una elipse, una parábola y una hipérbola, pero también un punto, una recta y un par de rectas que se cortan. Esta última clase de secciones cónicas se llaman cónicas degeneradas, y las cónicas no degeneradas son todas aquellas equivalentes a la circunferencia bajo transformaciones proyectivas (e incluso perspectivas). Podemos pensar que la geometría proyectiva de cónicas es bastante complicada, pero no es así, si olvidamos las diferencias entre circunferencias, elipses, hipérbolas y parábolas y somos capaces de concentrarnos en sus propiedades comunes podemos llegar a tener un conocimiento más profundo de ellas.

En términos simples, la geometría proyectiva nos permite concentrarnos en el cono y no en sus secciones. De hecho, el cono $x^2+y^2-z^2$ representado en la figura 1 está construido por rectas que pasan por el origen. Esta familia uniparamétrica de rectas se puede interpretar como una curva $\mathcal C$sobre el plano proyectivo. Recordemos que en la identificación de $\mathbb{R} P^2$con el plano $z=1$más la recta del infinito, la curva $\mathcal C$venía representada como una circunferencia.

Ejercicio 1.1 (10)   Sea $L\subset\mathbb{R}P^2$una recta proyectiva y sea $\varphi_L\colon\mathbb{R}P^2\setminus L\rightarrow\mathbb{R}^2$la carta afín asociada. Demostrar que la curva $\varphi_L(\mathcal C)$es una elipse, una parábola, o una hipérbola según si el número de puntos en la intersección de $L$ y $\mathcal C$es cero, uno, o dos respectivamente.

En lo que sigue, vamos a considerar la carta fijada y transformaremos la curva $\mathcal C$ por diferentes transformaciones proyectivas.

Ejercicio 1.2 (10)   Transformar el cono $x^2+y^2-z^2=0$ mediante las siguientes transformaciones lineales y escribir las ecuaciones de la intersección del cono resultante con el plano $z=1$.

$$1. \left ( \begin{array}{ccc} 2 & 0 & 0\\ 0 & 3 & 0\\ 0 & 0 & 1... ...( \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & -1& 1 \end{array}\right ) .$$

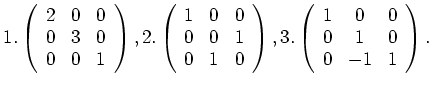
En las dos siguientes secciones introduciremos los conceptos algebraicos necesarios para estudiar cónicas y cuádricas proyectivas en los espacios de dimensión más alta.

Próximo: Conceptos algebraicos básicos Arriba: La Geometría Proyectiva de Anterior: La Geometría Proyectiva de