Próximo: Sobre
este documento ... Arriba:
La Geometría Proyectiva de Anterior: Cónicas reales sobre el
El modelo de Cayley-Klein para la geometría hiperbólica
Sea ![]() una cónica no degenerada y sea
una cónica no degenerada y sea ![]() el subgrupo de
transformaciones proyectivas que dejan la cónica invariante. El objetivo de los
próximos cuatro ejercicios es probar el siguiente resultado:
el subgrupo de
transformaciones proyectivas que dejan la cónica invariante. El objetivo de los
próximos cuatro ejercicios es probar el siguiente resultado:
Teorema 5.1 El grupo ![]() actúa transitivamente sobre el interior y
el exterior de la cónica
actúa transitivamente sobre el interior y
el exterior de la cónica ![]() .
.
Por los
resultados de la sección anterior, basta considerar el caso donde la cónica en
coordenadas homogéneas está dada por la ecuación ![]() .
.
La estrategia de la prueba es encontrar una clase
grande de transformaciones lineales explícitas sobre ![]() que conservan el cono
que conservan el cono ![]() , y demostrar que usando esta clase de
transformaciones es posible llevar una recta que pasa por el origen y está en
el interior (resp. exterior) del cono a cualquier otra recta que pasa por el
origen y está en el interior (resp. exterior) del cono.
, y demostrar que usando esta clase de
transformaciones es posible llevar una recta que pasa por el origen y está en
el interior (resp. exterior) del cono a cualquier otra recta que pasa por el
origen y está en el interior (resp. exterior) del cono.
Ejercicio 5.1 (-05) Definimos las funciones hiperbólicas
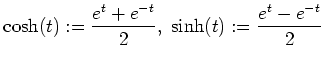
Probar que
1. ![]() ,
,
2. ![]() ,
,
3. ![]() ,
,
4.
La función ![]() es una biyección entre la
recta real y el intervalo
es una biyección entre la
recta real y el intervalo ![]() .
.
Si ![]() y
y ![]() son números reales, definimos
son números reales, definimos
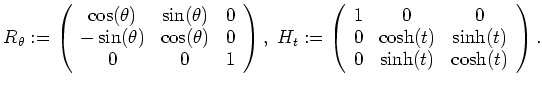
Ejercicio 5.2 (05) Probar que
1. ![]() .
.
2. ![]() y
y ![]() .
.
Ejercicio 5.3 (05) Probar que si ![]() pertenece al intervalo
pertenece al intervalo ![]() , existe un número
, existe un número ![]() tal que
tal que ![]() aplica el vector
aplica el vector ![]() en un
múltiplo no nulo del vector
en un
múltiplo no nulo del vector ![]() . Concluir que si
. Concluir que si ![]() , entonces existe un número
, entonces existe un número ![]() tal que
tal que ![]() aplica el vector
aplica el vector ![]() en un múltiplo no nulo del vector
en un múltiplo no nulo del vector ![]() .
.
El ejercicio
anterior implica fácilmente que ![]() actúa transitivamente sobre el interior de
actúa transitivamente sobre el interior de ![]() . En efecto, si
. En efecto, si ![]() y
y ![]() son dos rectas de que pasan por el
origen y dentro del cono
son dos rectas de que pasan por el
origen y dentro del cono ![]() , entonces existen rotaciones
, entonces existen rotaciones ![]() y
y ![]() tal que
tal que ![]() y
y ![]() están sobre el plano
están sobre el plano ![]() . Por el
ejercicio anterior, existe una transformación
. Por el
ejercicio anterior, existe una transformación ![]() tal que
tal que ![]() . Se sigue que
. Se sigue que ![]() , y con esto obtenemos
el resultado.
, y con esto obtenemos
el resultado.
Ejercicio 5.4 (10) Usar las mismas técnicas que antes para
demostrar que ![]() actúa transitivamente sobre el exterior de
actúa transitivamente sobre el exterior de
![]() .
.
Ahora pasamos al
estudio de la acción de ![]() sobre el interior de
sobre el interior de ![]() , que de ahora en adelante denotaremos como
, que de ahora en adelante denotaremos como ![]() . El primer comentario sobre esta acción es
que la acción no es doblemente transitiva: es, en el general, imposible
transformar un par de puntos distintos
. El primer comentario sobre esta acción es
que la acción no es doblemente transitiva: es, en el general, imposible
transformar un par de puntos distintos ![]() en un par de puntos prefijados
en un par de puntos prefijados ![]() . Como
antes, basta considerar el caso donde la cónica es una circunferencia.
. Como
antes, basta considerar el caso donde la cónica es una circunferencia.
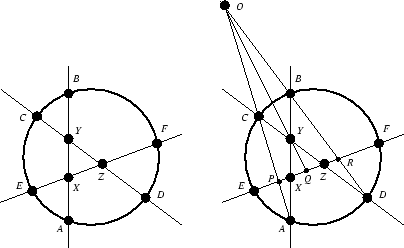
Si ![]() e
e ![]() son dos puntos
distintos de
son dos puntos
distintos de ![]() , dibujamos la recta que los une y cortamos
con la circunferencia para obtener dos puntos
, dibujamos la recta que los une y cortamos
con la circunferencia para obtener dos puntos ![]() y
y ![]() . Escogemos la notación
tal que
. Escogemos la notación
tal que ![]() pertenece al trozo de segmento
pertenece al trozo de segmento ![]() , e
, e ![]() pertenece al trozo de segmento
pertenece al trozo de segmento ![]() (fig 9). Ahora
definimos
(fig 9). Ahora
definimos ![]() . Nótese que hemos escogido este
orden (siguiendo la definición anterior de
. Nótese que hemos escogido este
orden (siguiendo la definición anterior de ![]() y
y ![]() )
para que esta razón doble sea mayor que uno. Si
)
para que esta razón doble sea mayor que uno. Si ![]() ,
definimos
,
definimos ![]() igual a uno.
igual a uno.
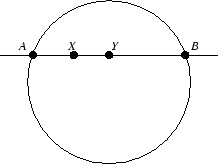
figura 9
Ejercicio 5.5 (15) Sean ![]() cuatro puntos sobre
cuatro puntos sobre ![]() . Demostrar existe una aplicación
. Demostrar existe una aplicación ![]() que lleva
que lleva ![]() a
a ![]() e
e ![]() a
a ![]() si y sólo si
si y sólo si ![]() .
.
Si ![]() e
e ![]() son dos puntos en
son dos puntos en ![]() , definimos
, definimos ![]() . El resto de esta sección se
dedica a probar que
. El resto de esta sección se
dedica a probar que ![]() es una función distancia y que sus geodésicas son las rectas.
es una función distancia y que sus geodésicas son las rectas.
Ejercicio 5.6 Probar que
1.
![]() y se da la igualdad si y sólo si
y se da la igualdad si y sólo si ![]() .
.
2. ![]() .
.
3.
Si ![]() son tres puntos
colineales, con
son tres puntos
colineales, con ![]() perteneciente al segmento que une
perteneciente al segmento que une ![]() y
y ![]() ,
entonces
,
entonces ![]() .
.
Para probar que ![]() es una función distancia, sólo queda comprobar
la desigualdad triangular para tres puntos no colineales
es una función distancia, sólo queda comprobar
la desigualdad triangular para tres puntos no colineales ![]() (fig 10). Como el logaritmo es una
función creciente, todo lo que debemos hacer es probar que
(fig 10). Como el logaritmo es una
función creciente, todo lo que debemos hacer es probar que ![]() , donde estas cantidades
son
, donde estas cantidades
son
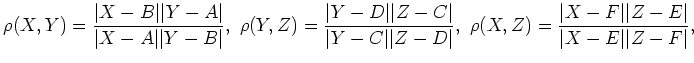
figuras 10 y
11
Usando la figura 11 y la invarianza de la razón doble
bajo perspectividades, tenemos que
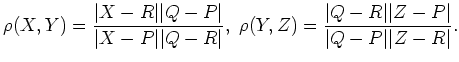
Por lo tanto,
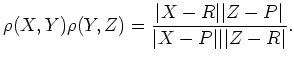
Ejercicio 5.7 Terminar la prueba de la desigualdad
triangular demostrando que
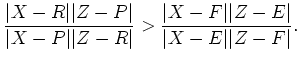
El disco ![]() junto con la distancia
junto con la distancia ![]() se llama el plano hiperbólico.
se llama el plano hiperbólico.
Definición
5.2
Sea ![]() un
espacio métrico y sea
un
espacio métrico y sea ![]() una curva continua. Definimos la longitud de
una curva continua. Definimos la longitud de ![]() como
como
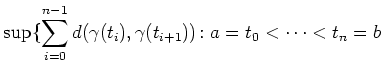 es una partición de
es una partición de ![]()
La curva ![]() se llama un segmento geodésico si su longitud es igual a la
distancia entre sus puntos finales.
se llama un segmento geodésico si su longitud es igual a la
distancia entre sus puntos finales.
Ejercicio 5.8 (10) Probar que cualquier segmento de recta
sobre ![]() es un segmento geodésico para la distancia
es un segmento geodésico para la distancia ![]() .
.
Próximo:
Sobre
este documento ... Arriba: La Geometría Proyectiva de Anterior:
Cónicas
reales sobre el