Introducción a la Geometría Proyectiva
Juan Carlos Álvarez Paiva
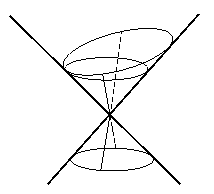
Geometría proyectiva de las cónicasUna sección cónica es, por definición, la imagen de una circunferencia bajo una perspectividad cuyo centro es el vértice del cono. Moviendo e inclinando el plano, podemos obtener una elipse, una parábola, y una hipérbola, pero también un punto, una recta, y un par de rectas que se cortan. Estas últimas secciones cónicas se llaman, en general, degeneradas; ya que las cónicas no degeneradas son aquellas equivalentes a la circunferencia bajo transformaciones proyectivas (e incluso perspectivas). Podemos pensar que la geometría proyectiva de las cónicas es bastante complicada. Al contrario, si olvidamos las diferencias entre circunferencias, elipses, hipérbolas, y parábolas, somos capaces de concentrarnos en sus propiedades comunes y tener un conocimiento más profundo de ellos.
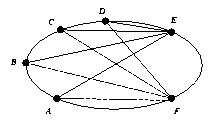
Como consecuencia de la equivalencia proyectiva de las cónicas, cualquier resultado de naturaleza proyectiva que podamos demostrar para la circunferencia, valdrá también para todas las cónicas. Un ejemplo fácil de tal resultado es el siguiente Proposición. Sean A, B, C, D cuatro puntos sobre una cónica. Si E y F son otros dos puntos sobre la misma cónica, diferentes de los de cuatro puntos anteriores, entonces las razones dobles [EA, EB, CE, ED] [ FA, FB, FC, FD] son iguales.
Comentamos que la razón doble de cuatro rectas que pasan por un punto X está definida como la razón doble de los cuatro puntos obtenidos al cortar estas rectas con una recta arbitraria que no pase por X. |
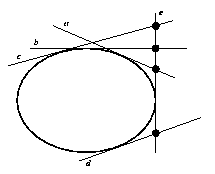
La dualidad proyectiva bidimensional no sólo intercambia puntos y rectas, sino que intercambia también el conjunto de puntos que están sobre una curva con el conjunto de rectas tangentes a la curva. Si sustituimos el punto de una cónica por la recta tangente a una cónica en la proposición anterior, obtenemos un nuevo resultado: Proposición. Sean a,b,c, d cuatro rectas tangentes a una cónica. Si e y f son dos rectas tangentes a la misma cónica diferentes de las anteriores, entonces las razones dobles [e.a, e.b, e.c, e.d] [ f.a, f.b, f.c, f.d] son iguales.
El dual de las proposiciones anteriores son los teoremas fundamentales en el estudio proyectivo de las cónicas. Son debidos a dos de los personajes más interesantes en la historia de las matemáticas: Jacob Steiner y Michel Chasles. El teorema de Steiner.
Si f es una transformación proyectiva entre el haz de rectas que pasan por
un punto X y el haz de rectas que pasan por un punto Y, entonces lugar
geométrico de los puntos {m.f
(m): m recta que pasa por X} Es una cónica. El teorema de Chasles.
Si f es una transformación proyectiva entre el conjunto de puntos que
están sobre una recta m y el conjunto de puntos que están sobre una recta l,
entonces el lugar geométrico de las rectas {Xf
(X): X punto sobre m} Es una cónica tangencial. No podemos resistir la tentación de mencionar un hermoso resultado de Chasles la cuya prueba va más allá del alcance de este curso, pero cuyo enunciado es muy simple: Teorema. El número de cónicas tangentes a cinco puntos prefijados en posición general es 3264. |
[Primera página][Página anterior][Página siguiente][Referencias][Geometría proyectiva][La página original de J.C. Alvarez]