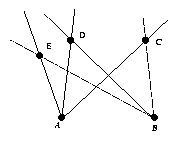
Geometría proyectiva de las cónicas (cont).

Seguimos nuestra revisión de la geometría proyectiva de las cónicas estableciendo algunas consecuencias simples de los teoremas principales de Chasles y Steiner. El primero es que cinco puntos (o cinco rectas) en posición general determinan una cónica. Para ver esto, consideremos los puntos A,B,C,D,E y sea f una transformación proyectiva entre el haz de rectas que pasan por A y el haz de rectas que pasan por B que llevan  AC en BC, AD en BD, y AE en BE. Por el primer teorema fundamental esta transformación existe y es única. Nótese que por el teorema de Steiner el lugar geométrico de los puntos

{m.f(m): m recta que pasa por A}

es una cónica. Se prueba fácilmente que esta cónica pasa por los cinco puntos prefijados.

Cinco puntos en la posición general determinan una cónica.

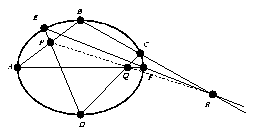
Otra consecuencia relativamente simple del teorema de Steiner es un teorema mucho más antiguo debido a Pascal.

El teorema de Pascal. Los seis vértices de un hexágono están sobre una cónica si y sólo si los tres puntos obtenidos por el corte de tres pares de lados enfrentados son colineales.

Pulsar aquí para applet.

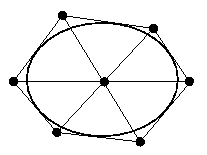
El teorema de Pascal también se puede usar como una manera de construir una cónica cuando se dan cinco de sus puntos. Pulse aquí para una demostración. El dual del teorema de Pascal dice así:

El teorema de Brianchon. Los seis lados de un hexágono son tangentes a una cónica si y sólo si las tres rectas obtenidas uniendo los tres pares de vértices enfrentados son concurrentes

El teorema de Brianchon es el dual de Pascal.