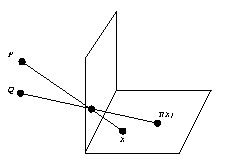
Transformaciones proyectivas en dimensión dos

Ahora consideramos las transformaciones del plano proyectivo (esto es, el plano más la recta del infinito) que son análogas a aquellas que ya consideramos sobre la recta proyectiva. Las composiciones de estas transformaciones se llamarán transformaciones proyectivas (del plano proyectivo).

Una clase de transformaciones sobre el plano proyectivo.

Como en el caso unidimensional, estamos interesados en saber como las transformaciones proyectivas mueven los puntos. Ya que estas transformaciones conservan rectas, no podemos esperar que tres puntos prefijados sean transformados en otros tres puntos prefijados. Puede ser que los tres primeros puntos sean colineales y los otros no. Sin embargo, si decimos que los cuatro puntos están en posición general cuando tres cualesquiera de ellos no están sobre la misma recta, tenemos el resultado siguiente:

Primer teorema fundamental. Si dos cuaternas de puntos A,B,C,D y A',B',C',D ' están en la posición general, existe una única transformación proyectiva del plano que lleva A a A', B a B', C a C', y D a D'.

En dimensión dos esta es la propiedad de llevar rectas a rectas que caracteriza las transformaciones proyectivas del plano.

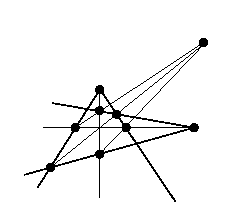
Segundo teorema fundamental. Si una biyección del plano proyectivo sobre sí mismo lleva rectas a rectas, entonces es una transformación proyectiva.

El principio de dualidad

Uno de los aspectos más interesantes de la geometría proyectiva en dimensión mayor que uno, es el principio de dualidad. Este principio afirma que los teoremas en la geometría proyectiva vienen a pares duales: por ejemplo, en dimensión 2, basta intercambiar las palabras  recta y punto, y cambiar la intersección de dos rectas por la recta que une dos puntos y viceversa. Por ejemplo, el dual del teorema de Desargues es su opuesto y el dual del teorema de Pappus es así:

Dual del teorema de Pappus. Si a,b,c y a',b ',c ' son dos ternas de rectas concurrentes, entonces las rectas (a.b ') (a '.b), (a.c ') (c.a '), (y b.c ') (c.b ') son concurrentes.

Pulse aquí para applet.

Este principio "mágico" no es en el fondo nada más que una interpretación geométrica de dualidad de espacios vectoriales.