Razones dobles

Sean A,B, C y D cuatro puntos  sobre la recta real ampliada (el infinito se añade como un punto ideal). Por el primer teorema fundamental, existe una y sólo una transformación proyectiva T que envía A al infinito, B al cero, y  C a 1. El número  T(D) es la razón doble de los cuatro puntos. Esto por lo general se denota por [A,B,C,D]. No es difícil ver que la razón doble de cuatro puntos es invariante en transformaciones proyectivas. Es decir, si A,B,C y D son cuatro puntos y S es una transformación proyectiva, entonces

[A,B,C,D] = [S(A),S(B),S(C),S(D)].

Podemos razonar así: Si T es la única transformación proyectiva que envía A al infinito, B al cero, y C a 1, entonces [A,B,C,D] =  T(D). Por otra parte si R es la única transformación proyectiva que envía S(A) al infinito, S(B) al cero, y  S (C) a 1, entonces [S(A), S(B), S(C),S(D)] =  R(S(D)). Como la composición TS^-1 también envía S(A) al infinito, S(B) al cero, y  S(C) a 1, tenemos que TS^-1 = R por el primer teorema y por tanto  R(S(D))=T(D).

Desde luego, sería útil saber calcular razones dobles. Y resulta que la fórmula es bastante simple: si x₀, x₁, x₂, y x₃  son las coordenadas de cuatro puntos sobre la recta real ampliada, entonces

La razón doble es el análogo proyectivo de distancia en la geometría Euclídea. Es el invariante que define la geometría:

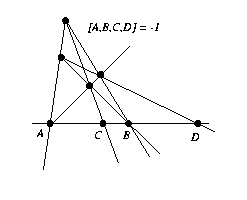
Segundo teorema fundamental. Si una transformación de la recta proyectiva conserva la razón doble, entonces es una transformación proyectiva.

En el siglo diecinueve había un lucha con la geometría analítica y algunos geómetras decidieron que el segundo teorema fundamental escrito arriba no era bastante geométrico. Para mejorarlo, aprovecharon una construcción geométrica para las cuaternas de puntos con razón doble igual a -1. Tales cuaternas se llaman  armónicas. Para entender la construcción paso a paso podemos pulsar sobre el siguiente gráfico. El applet le permitirá experimentar con la construcción. Por ejemplo, nótese que pasa cuando C es el punto medio del segmento AB.

El teorema de Von Staudt. Si una transformación de la recta proyectiva  se conserva por cuaternas armónicas, entonces es una transformación proyectiva.