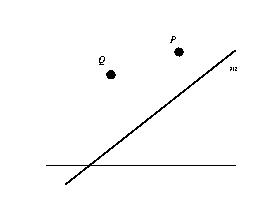
Transformaciones proyectivas

Para estudiar los invariantes de la geometría proyectiva más detalladamente, simplificamos la situación considerando una clase de transformaciones de la recta real sobre sí misma. Estas transformaciones se pueden describir de la siguiente forma: consideremos   una recta real dentro del plano, dibujemos una segunda recta m y dos puntos P y Q como en el gráfico siguiente. Si X es un punto sobre la recta real, su  imagen T (X) es la intersección de la recta real con la recta que pasa por el punto Q y la intersección de XP y  m (pulsa sobre la imagen). Si esta recta es paralela a la recta real decimos que la imagen de X es el punto del infinito.

Moviendo la recta m o los puntos P y la Q obtenemos muchas transformaciones diferentes. El lector puede experimentar este tipo de transformaciones usando el applet.

Una versión de más sencilla del problema de Alberti es: ¿cuáles son los invariantes de este tipo de transformaciones?.

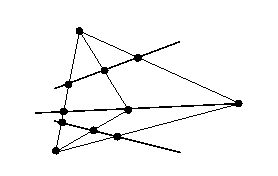
Una observación preliminar nos lleva a algo que parece casi trivial, pero que en realidad es muy importante:  cualquier cantidad que es invariante bajo estas transformaciones lo es también bajo su composición. Acordemos en llamar transformaciones proyectivas a todas las transformaciones posibles que se pueden obtener mediante la construcción anterior o mediante la composición de ellas  .

Para ver como una transformación proyectiva puede mover los puntos,  consideraremos primero dos rectas con tres puntos en cada una. No es difícil ver que combinando dos perspectivas es posible transformar los tres puntos de la primera recta en los tres puntos de la segunda recta. El siguiente gráfico da  la construcción. Si pulsamos sobre el, tendremos una construcción gradual.

Aplicando esta construcción dos veces para volver a la recta original, vemos que una transformación proyectiva puede llevar tres puntos prefijados en otros tres puntos prefijados. De hecho, es cierto algo más:

Primer teorema fundamental. Si A,B,C y A',B',C' son dos ternas de puntos distintos que están sobre una recta, hay una y sólo una transformación proyectiva que envía A a A', B a B', y C a C'.

El inconveniente de este resultado es que no puede haber ningún invariante de transformaciones proyectivas que implique solamente tres puntos. Vamos a intentarlo ahora con cuatro puntos.