Puntos y rectas en el infinito

El método de proyección y sección tiene una pequeña peculiaridad, ya que hay algunos puntos de una representación que parecen no tener ninguna imagen en la otra. Por ejemplo, en la figura siguiente bidimensional, el punto  B parece no tener ninguna imagen.

La manera clásica de resolver esta dificultad es decretar como imagen de B el  punto del infinito sobre la recta m. Esta noción de puntos ideales puede parecer, en principio, problematica, pero dejaremos esto para más adelante (véase el capítulo dos del curso interactivo de geometría proyectiva). El mismo fenómeno aparece en la siguiente figura, pero aquí es una recta entera de puntos sobre el plano vertical la que no tiene ninguna imagen sobre el plano horizontal. La imagen de esta recta, se dice que es la recta del infinito sobre el plano horizontal. La recta junto con su punto ideal en el infinito se llamará la recta proyectiva, y el plano con su recta ideal en el infinito se dirá el plano proyectivo.

Invariantes

Siempre que tenemos una clase de transformaciones, en nuestro caso las  obtenidas por proyección y sección, es interesante estudiar qué propiedades se conserva y cuales no por estas transformaciones. Se llaman invariantes las propiedades que se conservan y la mayor parte de matemáticas y la física consiste en su estudio.

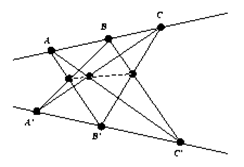
El problema planteado por Alberti es  determinar los invariantes de la perspectiva. Es claro que las distancias no se conservan, ni tampoco los ángulos, ni las áreas. Las rectas paralelas no se transforman en rectas paralelas. Esta capacidad para la deformación de imágenes puede llevarnos a pensar que la geometría proyectiva es difícil de estudiar. Pero no es así: las rectas van a rectas y si un punto está sobre una recta, entonces desde cualquier otro punto de vista el punto correspondiente estará sobre la recta en cuestión. Diremos que se conserva la incidencia. Puede parecer que esto no es mucho, pero es suficiente para desarrollar una teoría matemática de gran poder y belleza.

Dos resultados clásicos que dependen únicamente de la noción de incidencia son los teoremas de Pappus y Desargues. Antes de enunciarlos, fijemos alguna notación. La recta que une dos puntos X e Y la denotaremos por XY, mientras que el punto de intersección de las rectas a y b lo escribiremos a.b.

El teorema de Pappus. Si A,B,C y A', B',C' son dos ternas de puntos colineales, entonces los puntos AB'.BA', AC'.CA', Y BC'.CB' son colineales.

Pulsa aquí para ver el applet.

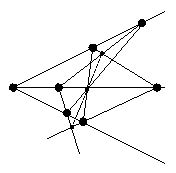
Teorema de Desargues. Si dos triángulos están en perspectiva, entonces sus lados correspondientes se cortan en tres puntos colineales.

Pulse aquí para applet.