Próximo: Los teoremas fundamentales Arriba: El plano proyectivo real Anterior: Conceptos básicos

Geometría proyectiva versus geometría afín

Como se explicó al final del capítulo uno (ejercicio 2.9), una transformación afín sobre $\mathbb{R}^n$es un par $(A,y)$ que consiste en una matriz $n\times n$ invertible $A$ y un vector $y$. Si $x$ es un punto en $\mathbb{R}^n$, la acción de $(A,y)$ sobre $x$ es $Ax+y$.

Ejercicio 2.1 (10) Sea $(A,y)$ una transformación afín sobre $\mathbb{R}^n$ y sea $B$ la matriz $(n+1)\times (n+1)$

$$\left ( \begin{array}{cccc} a_{11} & \cdots & a_{1n} & y_1\... ...ots & a_{nn} & y_n\\ 0 & \cdots & 0 & 1 \end{array}\right ).$$

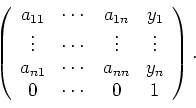
Probar que identificando $U_{n+1}$ con $\mathbb{R}^n$vía la carta $\varphi_{n+1}$ la transformación proyectiva definida por $B$es igual a la transformación afín definida por $(A,y)$.

Ejercicio 2.2 (15)   Usando el ejercicio anterior justificar la siguiente afirmación: el grupo de transformaciones afines sobre $\mathbb{R}^n$es el subgrupo de transformaciones proyectivas que fijan el hiperplano del infinito.

La noción de paralelismo es típica de geometría afín. Esto se puede interpretar fácilmente en la geometría proyectiva si fijamos el hiperplano en el infinito.

Ejercicio 2.3 (05)   Usar la figura 2 para demostrar que dos rectas en el plano $z=1$ son paralelas si y sólo si las rectas proyectivas correspondientes se cortan en el infinito.

 

figura 2

 

Ejercicio 2.4 (00)   Probar que dos subespacios afines en $\mathbb{R}^n$son paralelos si y sólo si todos los puntos de su intersección están en el hiperplano del infinito.

Parte de la filosofía de la geometría proyectiva está pensar $\mathbb{R}^n$como un subconjunto de $\mathbb{R}P^n$. Equivalentemente, podemos decir que $\mathbb{R}P^n$es una compactificación de $\mathbb{R}^n$. Este punto de vista es práctico en la resolución de muchos problemas geométricos. El siguiente ejercicio es un bonito ejemplo:

Ejercicio 2.5 (25)   Un conjunto convexo en $\mathbb{R}^n$es el que contiene cada segmento de recta que une cualesquiera dos de sus puntos. Por ejemplo un disco es convexo, pero un croissant no lo es. Demostrar que cualquier subconjunto ilimitado convexo sobre el plano contiene una semirrecta.

De la misma manera, algunos teoremas de geometría proyectiva son más fáciles de demostrar si los reducimos a teoremas en la geometría afín. Ejemplos clásicos son los teoremas de Pappus y Desargues, los cuales hemos escrito en forma de ejercicios.

Nota. En las construcciones geométricas que siguen, denotaremos los puntos por letras mayúsculas y las rectas por letras minúsculas. El símbolo $AB$denota la recta que pasa por los puntos $A$ y $B$, mientras $a\cdot b$ denota el punto de intersección de las rectas $a$ y $b$.

Teorema 2.1 (Pappus)   Dibujamos dos rectas sobre el plano proyectivo y tres puntos sobre cada recta. Denotamos $A$,$B$ y $C$ los puntos de la primera recta, y $A'$,$B'$ y $C'$ los puntos sobre la segunda. Dibujamos las rectas que unen los puntos denotados por letras diferentes (esto es, no dibujamos las rectas $AA'$, ni $BB'$, ni $CC'$). Entonces los puntos $AB'\cdot BA'$, $AC'\cdot CA'$ y $BC'\cdot CB'$ son colineales.

 

figura 3

 

 

La demostración se da en los siguientes dos ejercicios. En el primero se debe demostrar la versión afín del teorema.

Ejercicio 2.6 (10)   Dibujemos dos rectas sobre el plano. Sean $A$, $B$ y $C$puntos sobre la primera recta, y $A'$,$B'$ y $C'$puntos sobre la segunda recta tal que $AB'$es paralelo a $BA'$, y $BC'$es paralelo a $CB'$. Probar que $AC'$es necesariamente paralelo a $CA'$.

 

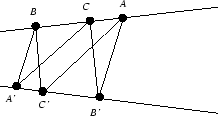
figura 4

Ahora viene la reducción del resultado proyectivo al resultado afín.

Ejercicio 2.7 (10)   Sea $\mathcal T$cualquier transformación proyectiva que envía los puntos $AB'\cdot BA'$y $BC'\cdot CB'$ al infinito. Aplicar $\mathcal T$a los puntos y rectas en la configuración del teorema 2.1 y comprobar que la nueva configuración es igual que la del ejercicio anterior. Usar esto para demostrar el teorema de Pappus.

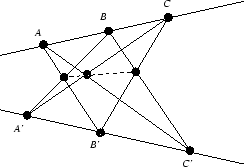
Teorema 2.2 (Desargues)   Dibujemos las rectas $a$, $b$ y $c$ sobre el plano proyectivo, y consideremos los puntos $A,A'\in a$,  $B,B'\in b$ y $C,C'\in c$. Entonces los puntos $AB\cdot A'B'$, $AC\cdot A'C'$ y $BC\cdot B'C'$ son colineales si y sólo si las rectas $a$, $b$ y $c$ son concurrentes.

 

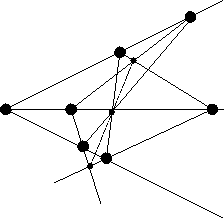
figura 5

 

Ejercicio 2.8 (20)   Escribir y demostrar una versión afín del teorema de Desargues. Reducir el teorema de Desargues a su versión afín usando una transformación proyectiva adecuada.

Vamos a presentar ahora otra demostración de estos resultados usando el teorema de incidencia que pasamos a enunciar:

Teorema 2.3 (de incidencia)   Sean $P(W)$y $P(W')$ dos subespacios proyectivos de $\mathbb{R}P^n$entonces se tiene:

$$dim((P(W))+dim(P(W'))=dim((P(W)+P(W'))+dim((P(W)\cap P(W'))$$

Ejercicio 2.9 (05)   Demostrar el teorema 2.3.

Ejercicio 2.10 (15)   Probar los teoremas de Pappus y Desargues usando el teorema de incidencia.

Próximo: Los teoremas fundamentales Arriba: El plano proyectivo real Anterior: Conceptos básicos