Próximo: Bibliografía Arriba: El plano proyectivo real Anterior: Geometría proyectiva versus geometría

Los teoremas fundamentales

En el capítulo dos, hemos visto que una transformación proyectiva de la recta proyectiva está completamente determinada por las imágenes de tres puntos distintos. El análogo en dimensiones superiores de este resultado hace uso de la noción sistema de referencia proyectivo.

Definición 3.1   Una $(n+2)$-upla de puntos $\{p_1,\cdots ,p_n+2\}$ en $\mathbb{R}P^n$es un sistema de referencia proyectivo si existe una base $\{v_1,\cdots ,v_n+1\}$de $\mathbb{R}^{n+1}$ tal que $p_i=[v_i]$ para $1<i<n+1$ y  $p_{n+2}=[v_1+\cdots v_{n+1}]$. La base $\{v_1,\cdots ,v_n+1\}$ se llama base de determinación del sistema de referencia proyectivo.

Ejercicio 3.1 (10)   Probar que cuatro puntos en $\mathbb{R}P^2$ forman un sistema de referencia proyectivo si y sólo si tres cualesquiera de ellos no están alineados.

Ejercicio 3.2 (*15)   Demostrar los teoremas de Pappus y Desargues usando sistemas de referencia proyectivos. Nota: Tener cuidado a la hora de elegir que puntos formarán nuestro sistema de referencia, tomar el más sencillo posible.

Teorema 3.2 (Primer teorema fundamental)   Si $\{p_1,\cdots ,p_n+2\}$ y $\{q_1,\cdots ,q_n+2\}$ son dos sistemas de referencia proyectivos en $\mathbb{R}P^n$, entonces existe una única transformación proyectiva $T\in PGL(n+1,\mathbb{R})$ tal que $T(p_i)=q_i$, $1<i<n+2$.

La demostración depende del siguiente sencillo ejercicio .

Ejercicio 3.3 (10)   Sean $\{v_1,\cdots ,v_n+1\}$ y $\{w_1,\cdots ,w_n+1\}$ dos bases de $\mathbb{R}^{n+1}$ que son bases de determinación del mismo sistema de referencia proyectivo. Demostrar que existe un número real no nulo $\lambda$tal que $\lambda v_i=w_i$ para todo $i=1,\cdots ,n+1$.

Ejercicio 3.4 (05)   Demostrar el teorema 3.1.

Teorema 3.3 (Segundo teorema fundamental)   Sea $T\colon\mathbb{R}P^n\rightarrow \mathbb{R}P^n$ una biyección. Si $T$lleva rectas proyectivas a rectas proyectivas, entonces es una transformación proyectiva.

Para hacer las cosas más sencillas, demostraremos este teorema sólo en el caso $n=2$. Se deja al lector ampliar la demostración a dimensiones arbitrarias. Realizamos una serie de reducciones antes de llegar a un problema en geometría afín.

Ejercicio 3.5 (05)   Supongamos que una biyección $T\colon\mathbb{R}P^2\rightarrow \mathbb{R}P^2$ que lleva rectas proyectivas a rectas proyectivas, y fija los puntos $[1:0:0]$, $[0:1:0]$, $[0:0:1]$  y $[1:1:1]$ es la identidad. Demostrar que esto implica el segundo teorema fundamental.

De ahora en adelante, consideraremos el plano proyectivo como el plano $z=1$ más la recta del infinito (véase la figura 1). También identificaremos el plano $z=1$ con $\mathbb{R}^2$. Dicho de otra forma, usaremos la carta $\varphi_z\colon U_z\rightarrow\mathbb{R}^2$ y veremos $\mathbb{R}P^2/U_z$ como la recta del infinito.

Ejercicio 3.6 (15)   Probar que una biyección $T\colon\mathbb{R}P^2\rightarrow \mathbb{R}P^2$ que lleva rectas proyectivas a rectas proyectivas, y fija los puntos $[1:0:0]$, $[0:1:0]$, $[0:0:1]$ y  $[1:1:1]$, satisface también las propiedades siguientes:

1.    La restricción de $T$ a $U_z$ es una biyección de $U_z\equiv\mathbb{R}^2$.

2.    Como biyección de $\mathbb{R}^2$, $T$ lleva rectas a rectas y paralelas a paralelas.

3.    $T$ deja fijos el eje $x$ el eje $y$, y la diagonal $x=y$.

4.    $T$ fija el origen de $\mathbb{R}^2$y el punto $(1,1)$.

Ejercicio 3.7 (05)   Probar que $T$ fija los puntos $(1,0)$y $(0,1)$.

Ahora definimos $\sigma_x\colon\mathbb{R}\rightarrow\mathbb{R}$ mediante la ecuación $T(\lambda t,0)=(\sigma_x(\lambda)t,0)$. Se sigue inmediatamente de los ejercicios anteriores que $\sigma_x(0)=0$ y $sigma_x(1)=1$.

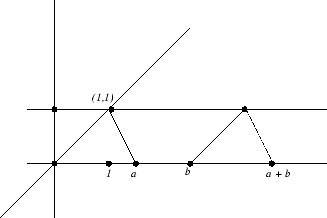
Ejercicio 3.8 (15)   Usar la construcción dada en la figura 6 de la suma de dos números reales usando rectas paralelas para demostrar que $\sigma_x(a+b)=\sigma_x(a)+sigma_x(b)$.

 

figura 6

 

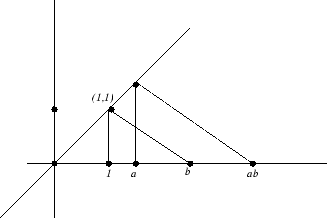
Ejercicio 3.9 (15)   Usar la construcción dada en la figura 7 de la multiplicación de dos números reales usando rectas paralelas para demostrar que $\sigma_x(a\cdot b)=\sigma_x(a)\cdot sigma_x(b)$.

 

Como consecuencia de estos ejercicios, tenemos que $\sigma_x$es un automorfismo de $\mathbb{R}$ y, por tanto, igual a la identidad. Si definimos $\sigma_y$ por la ecuación $T(0,\lambda t)=(0,\sigma_y(\lambda)t)$, entonces los mismos argumentos demuestran que $\sigma_y$ es la identidad. Ahora el toque final:

Ejercicio 3.10 (10)   Usar que $T$ lleva rectas paralelas a rectas paralelas y fija los ejes $x$ e $y$ punto a punto para concluir que $T$es la identidad.

Próximo: Bibliografía Arriba: El plano proyectivo real Anterior: Geometría proyectiva versus geometría