Próximo: Geometría proyectiva versus geometría Arriba: El plano proyectivo real Anterior: El plano proyectivo real

Conceptos básicos

Definición 1.1   Si $W\subset\mathbb{R}^{n+1}$ es un subespacio vectorial, el conjunto de todas las rectas de $W$ que pasan por el origen es un subespacio proyectivo de $\mathbb{R}P^n$que denotaremos por $P(W)$. Si la dimensión de $W$ es igual a $k+1$, decimos que $P(W)$ es un subespacio proyectivo $k$-dimensional. A un subespacio proyectivo de dimensión uno lo llamaremos una recta proyectiva y un subespacio proyectivo de codimensión uno lo llamaremos un hiperplano proyectivo.

Ejercicio 1.1  

1.    Probar que las transformaciones proyectivas de $\mathbb{R}P^n$ llevan subespacios proyectivos $k$-dimensionales a subespacios proyectivos $k$-dimensionales.

2.    Definir la suma y la intersección de subespacios proyectivos.

Ejercicio 1.2 (* 05)   Sea $V$un espacio vectorial de dimensión cuatro sobre un cuerpo $\mathbb{F}$con $p$ elementos. ¿Cuántas rectas proyectivas hay entonces en $P(V)$? ¿Cuántos hiperplanos proyectivos?

Ejercicio 1.3 (10)   Comprobar que las rectas proyectivas en $\mathbb{R}P^2$ tienen las dos siguientes propiedades:

• Cualesquiera dos rectas proyectivas se cortan en un punto.
• Cualesquiera dos puntos distintos se unen por una única recta proyectiva.

La figura 1 muestra que el conjunto de rectas de $\mathbb{R}^3$que pasan por el origen y no son horizontales puede ser identificado con el conjunto de puntos sobre el plano $z=1$. Nótese también que una recta sobre el plano se corresponde con una recta proyectiva sobre $\mathbb{R}P^2$.

 

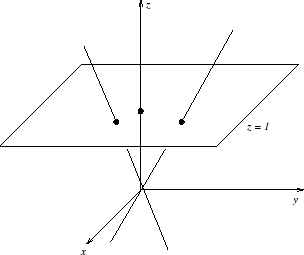
Figura 1

 

Ejercicio 1.4 (00)   Probar que $\mathbb{R}P^2$ menos una recta proyectiva se identifica con $\mathbb{R}^2$.

La versión analítica de la figura anterior se da en el siguiente ejercicio:

Ejercicio 1.5   1.5 (00) Sea $U_z$ el conjunto del plano proyectivo cuyas coordenadas homogéneas $[x:y:z]$ cumplen $z\neq 0$ (estos se corresponden a las rectas en $\mathbb{R}^3$que pasan por el origen y no son horizontales). Demostrar que la aplicación $\varphi_z\colon U_z\rightarrow\mathbb{R}^2$ dada por $[x:y:z]\mapsto (x/z,y/z)$ es una biyección.

Ejercicio 1.6 (10)   Consideremos ahora $\mathbb{R}P^n$ y definimos $U_i\subset \mathbb{R}P^n$como el conjunto de puntos cuyas coordenadas homogéneas $[x_1:\cdots :x_{n+1}]$ cumplen $x_i\neq 0$. Probar que

1.    La unión de los $U_i$,  $1<i<n+1$, es todo $\mathbb{R}P^n$.

2.    La aplicación $\varphi_i\colon U_i\rightarrow\mathbb{R}P^n$ dada por

$$[x_1:\cdots :x_{n+1}]\mapsto (x_1/x_i,\cdots ,x_{i-1}/x_i,x_{i+1}/x_i,\cdots ,x_{n+1}/x_i)$$

es una biyección.

3.    Calcular la aplicación $\varphi_i\circ\varphi_j^{-1}$ definida sobre $\varphi(U_i\cap U_j)\subset \mathbb{R}^n$.

Las aplicaciones $\varphi_i\colon U_i\rightarrow\mathbb{R}^n$ se llaman cartas y se pueden usar para trabajar sobre el espacio proyectivo como si fuese $\mathbb{R}P^n$. Cuando hacemos esto, el hiperplano proyectivo dado por todos los puntos cuyas coordenadas homogéneas son de la forma $[x_1:\cdots :x_{i-1}:0:x_{i+1}:\cdots :x_{n+1}]$ se llama el hiperplano del infinito (visualizarlo en la figura 1). Estos son exactamente los puntos que no están en $U_i$ y no se tienen en cuenta en nuestra representación. Como probamos en el siguiente ejercicio, podemos elegir cualquier hiperplano proyectivo como nuestro hiperplano del infinito.

Ejercicio 1.7 (05)   Deducir del ejercicio anterior que si $P(W)\subset\mathbb{R}^n$es un hiperplano proyectivo, entonces $\mathbb{R}P^n/P(W)$ se puede identificar con $\mathbb{R}^n$. Dar una prueba gráfica en el caso $n=2$.

Ahora describimos la acción de $PGL(n+1,\mathbb{R})$ utilizando las cartas de $\mathbb{R}P^n$. Para hacer las cosas más sencillas, consideraremos únicamente la carta $\varphi_{n+1}$ . En este caso decimos que trabajamos en un sistema de coordenadas adaptado. Aunque la idea de sistemas de coordenadas la introduciremos más adelante.

Si $A$es una matriz invertible $(n+1)\times (n+1)$, entonces su acción sobre $\mathbb{R}P^n$en coordenadas homogéneas está dada simplemente por $[v]\mapsto [Av]$. Si $(y_1,\cdots y_n)\in\mathbb{R}^n$lo identificaremos con el punto $[y_1:\cdots :y_n:1]\in\mathbb{R}P^n$. La matriz $A$ envía este punto al punto

$$[\sum_{i=1}^n a_{1,i}y_i+a_{1,n+1}:\cdots :\sum_{i=1}^n a_{n+1,i}y_i+a_{n+1,n+1}]\in\mathbb{R}P^n.$$

Si usamos $\varphi_{n+1}$ para identificar este punto con un punto en $\mathbb{R}^n$, obtenemos $(x_1,\cdots x_n)$, donde

$$x_i:=\frac{a_{i,1}y_1+\cdots +a_{i,n}y_n+a_{i,n+1}} {a_{n+1,1}y_1+\cdots +a_{n+1,n}y_n+a_{n+1,n+1}}.$$

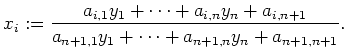
Cuando el denominador se anula, diremos que el punto $(y_1,\cdots ,y_{n+1})$ va al infinito.

Próximo: Geometría proyectiva versus geometría Arriba: El plano proyectivo real Anterior: El plano proyectivo real