Siguiente: Clasificación proyectiva y afín Subir: Estudio Euclídeo Anterior: Geometría en dos dimensiones

Geometría euclídea de las cónicas

Empezamos considerando $I$, $J$ los puntos absolutos cuyas coordenadas serán $(1,i,0)$ y $(1,-i,0)$ respectivamente.

Ejercicio 3.6 (05)   Usando la involución del ejercicio 2.9, probar que en una cónica con centro hay un par de diámetros conjugados que son perpendiculares.

Definición 3.7   Estos diámetros especiales se llaman ejes.

Ejercicio 3.8 (05)   Probar que los ejes de una cónica forman un sistema de referencia rectangular donde la ecuación de la cónica se escribe:

$$aX^2+bY^2=1$$

Ejercicio 3.9 (10)   Probar que el único caso donde hay más de una pareja de ejes es la circunferencia.

Ejercicio 3.10 (10)  

• Probar que todos los puntos de la circunferencia equidistan del centro.
• Una cónica con centro es una circunferencia si y sólo si pasa por los puntos absolutos.

Definición 3.11   Un punto $F$ se dice foco de una cónica $C$ si las rectas de isotropía que pasan por $F$ son tangentes a $C$.

Definición 3.12   La recta polar de un foco $F$ de $C$ se llama directriz asociada al foco.

Ejercicio 3.13 (10)   Probar que una cónica con centro tiene cuatro focos, dos reales y otros dos complejos conjugados. Los focos reales están en un eje y los complejos en el otro. Véase la figura 2.

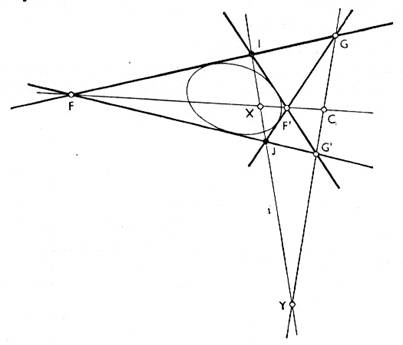
figura 2

 

Definición 3.14   Los puntos de corte de los ejes con la cónica se llaman vértices.

Ejercicio 3.15 (10)   Probar que el eje de una parábola y la recta tangente en el vértice son perpendiculares.

Siguiente: Clasificación proyectiva y afín Subir: Estudio Euclídeo Anterior: Geometría en dos dimensiones