Próximo: Acciones de grupos sobre Arriba: Grupos Anterior: Motivación y definiciones básicas

Ejemplos importantes del álgebra lineal

El estudio de grupos en geometría se reduce, por lo general, a los grupos de matrices. El ejemplo más simple es el grupo de matrices invertibles $1\times 1$. Esto es simplemente el conjunto de números reales no nulos con su multiplicación estándar. El análogo en dimensiones más altas es el grupo de matrices invertibles $n\times n$ junto con su multiplicación habitual.

Antes de seguir adelante, es necesario asegurarse de que podemos resolver sin esfuerzo los siguientes ejercicios:

Ejercicio 1.4   Multiplicar las matrices

$$\left ( \begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 ... ...& 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right )^{-1}$$

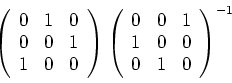
Ejercicio 1.5   Calcular mentalmente la inversa de la matriz

$$\left ( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 ... ...} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array}\right )$$

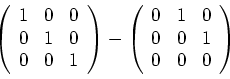
Ejercicio 1.6   Calcular el determinante de

$$\left ( \begin{array}{ccc} 1 & 1 & 0 \\ 5 & 1 & 1 \\ 2 & 0 & 1 \end{array}\right ) ^{-5}$$

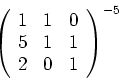
Si no se puede resolver estos problemas en un breve espacio de tiempo, entonces no está listo para este curso. Debería ponerse en contacto con el profesor.

Además del grupo $GL(n,\mathbb{R})$de matrices $n\times n$ invertibles de números reales, también tenemos el grupo $GL(n,\mathbb{C})$de matrices $n\times n$ invertibles de números complejos. Nótese que $GL(n,\mathbb{R})$es un subgrupo de $GL(n,\mathbb{C})$. De hecho, casi todos los grupos interesantes en la geometría son subgrupos de $GL(n,\mathbb{C})$. Hay algunos ejemplos:

El grupo lineal especial: El conjunto de matrices $n\times n$ reales (resp. complejas) cuyo determinante es igual a uno. Se denota por $SL(n,\mathbb{R})$( Resp. $SL(n,\mathbb{C})$) y se llama el grupo lineal especial. Si $A\in SL(n,\mathbb{R})$, Entonces la transformación de $\mathbb{R}^n$definida por $v\mapsto AV$conserva el volumen y la orientación.

El grupo ortogonal y el grupo ortogonal especial: Una matriz cuadrada, se dice que es ortogonal si su traspuesta es igual a su inversa. El conjunto de matrices $n\times n$ortogonales se denota por $O(n)$. El subconjunto de $O(n)$ formado por las matrices de determinante uno se denota $SO(n)$. Estos dos grupos se llaman el grupo ortogonal y el grupo ortogonal especial, respectivamente.

Ejercicio 1.7 (05)   Denotemos el producto escalar o interior de dos vectores $v$ y $w$en $\mathbb{R}^n$por $v\cdot w$.

Probar que si $A$ es una matriz $n\times n$ y $A^t$es su matriz traspuesta, entonces $Av\cdot w=v\cdot A^tw$. Concluir que si $A\in O(n)$, entonces $Av\cdot Aw=v\cdot w$. Probar que si $A$ es una matriz ortogonal, la distancia entre $v$ y $w$es igual a la distancia entre $Av$ y $Aw$. Probar que el determinante de una matriz ortogonal es $1$ o $-1$.

El grupo unitario y el grupo unitario especial: Si $A$es una matriz cuadrada de números complejos, el adjunto de $A$, denotado por $A^*$, es el resultado de trasponer y luego conjugar todas sus entradas. Por ejemplo

$$\left ( \begin{array}{cc} 1+i & 0 \\ i & 1 \end{array}\ri... ...t ( \begin{array}{cc} 1-i & -i \\ 0 & 1 \end{array}\right )$$

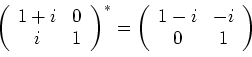
Una matriz cuadrada compleja se dice que es unitaria si su adjunta es igual a su inversa. El conjunto de matrices $n\times n$ unitarias se denota por $U(n)$. El subconjunto de $U(n)$que consiste en las matrices de determinante uno se denota por $SU(n)$. Se llaman respectivamente el grupo unitario y el grupo unitario especial.

Ejercicio 1.8 (05)   Definimos el producto hermitiano de dos vectores $v:=(v_1,\cdots ,v_n)$  y $w:=(w_1,\cdots ,w_n)$ en $\mathbb{C}^n$por $<v,w>=v_1\overline{w_1}+\cdots +v_n\overline{w_n}$.

1.    Probar que si $A$es una matriz $n\times n$ compleja y $A^*$es su matriz adjunta, entonces $<Av,w>=<v,A^*w>$. Concluir que si $A$es unitaria, entonces

$$<Av,Aw>=<v,w>.$$

2.    Probar que si $A$es una matriz unitaria, la distancia entre $v$ y $w$es igual a la distancia entre $Av$ y $Aw$.

3.    Probar que el determinante de una matriz unitaria es un número complejo de módulo uno.

Ejercicio 1.9 (*10)   En lo que sigue $I_n$denotará la matriz identidad $n\times n$ y $J_{2n}$es la matriz $2n\times 2n$ dada por

$$\left ( \begin{array}{cc} 0 & I_n \\ -I_n & 0 \end{array}\right )$$

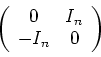
1.    Probar que el conjunto de todas las matrices $2\times 2$ reales que conmutan con $J_2$ se puede identificar de forma natural con el conjunto de los números complejos.

2.    Por la analogía con el apartado anterior, demostrar que el grupo $GL(n,\mathbb{C})$se puede ver como un subgrupo de $GL(2n,\mathbb{R})$.

3.    Definimos el producto simpléctico de dos vectores sobre $\mathbb{R}^{2n}$mediante $\omega(v,w)=v^tJw$. Demostrar que el producto simpléctico es antisimétrico y no degenerado.

4.    Definimos el grupo lineal simpléctico $Sp(2n)$ como el conjunto todas las matrices $2n\times 2n$ reales $A$ que satisfacen $A^tJA=J$. Demostrar que la intersección de $Sp(2n)$ y $GL(n,\mathbb{C})$es igual a $U(n)$.

Ejercicio 1.10 (15)   Probar que el grupo $SU(2)$se puede identificar con la esfera unidad  $3$-dimensional en $\mathbb{C}^2=R^4$.

Definición 1.3   La traza de una matriz cuadrada es la suma de todos los elementos de su diagonal. El conmutador de dos matrices $n\times n$$X$e $Y$, se denota por $[X,Y]$, y se define como $XY-YX$.

Ejercicio 1.11 (05)   En lo que sigue $A$, $X$e $Y$son matrices $n\times n$ con $A$ invertible.

1.    Probar que $[AXA^{-1},AYA^{-1}]=A[X,Y]A^{-1}$.

2.    Probar que si $X$tiene traza cero, entonces $AXA^{-1}$también tiene traza cero.

El siguiente ejercicio lo hemos tomado del libro de Abraham y Marsden sobre los fundamentos de mecánica (véase [1]).

Ejercicio 1.12 (15)   Sea $su(n)$el conjunto de matrices $n\times n$complejas de traza cero $X$ tal que $X^*=-X$.

1.    Probar que $su(n)$es un espacio vectorial y calcular su dimensión.

2.    Probar que si $A\in SU(n)$y $X\in su(n)$, entonces $AXA^{-1}\in su(n)$.

3.    Las tres matrices spin de Pauly de la mecánica cuántica son

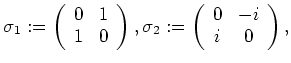$$\sigma_1:=\left ( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right ), \sigma_2:=\left ( \begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right ),$$   y$$~~~ \sigma_3:=\left ( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right ),$$

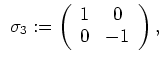
Probar que las matrices $\gamma_i=(i/\sqrt{2})\sigma_i$, $i=1,2,3$ forman una base de $su(2)$con las relaciones de conmutación

$$[\gamma_i,\gamma_j]=\epsilon_{ijk}\gamma_k$$

Donde $\epsilon_{ijk}$es igual a $1$si $ijk$ es una permutación par de $123$ y $-1$ si no lo es.

4.    Identificar $\mathbb{R}^3$con $su(2)$asignando a cada vector $x=(x_1,x_2,x_3)$la matriz

$$x\cdot\gamma=x_1\gamma_1+x_2\gamma_2+x_3\gamma_3.$$

Si $x\wedge y$denota el producto vectorial de dos vectores en $\mathbb{R}^3$, Probar que

$$[(x\cdot\gamma),(y\cdot\gamma)]=(x\wedge y)\cdot\gamma.$$

5.    Probar que el determinante de $(x\cdot\gamma)$es igual a $\frac{1}{2}\vert\vert x\vert\vert^2$.

6.    Sea $A$ en $SU(2)$y consideremos la transformación $T_A$de $\mathbb{R}^3$en sí mismo definida por $A(x\cdot\gamma)A^{-1}=T_Ax\cdot\gamma$. Probar que $T_A$es una transformación lineal que conserva distancias y tiene determinante igual a uno.

7.    Probar que si $A$ y $A'$están en $SU(2)$, entonces $T_A=T_A'$si y sólo si $A=A'$.

De este ejercicio concluimos que el grupo $SU(2)$, que vimos antes identificado con la $3$-esfera, tiene una correspondencia natural $2$ a $1$con el grupo de rotaciones $SO(3)$.

Próximo: Acciones de grupos sobre Arriba: Grupos Anterior: Motivación y definiciones básicas