Próximo: Bibliografía Arriba:
Grupos y sus acciones Anterior: Ejemplos importantes del álgebra
Acciones de grupos sobre conjuntos
Los grupos en geometría se definen a menudo como los
subgrupos del grupo de biyecciones de un conjunto. Sin embargo, una definición
abstracta de lo que significa la acción de un grupo sobre un conjunto también
es útil.
Definición
1.4
Sea ![]() un conjunto y sea
un conjunto y sea ![]() un grupo. Una acción (a la izquierda)
de
un grupo. Una acción (a la izquierda)
de ![]() sobre
sobre ![]() es una aplicación
es una aplicación ![]() tal que
tal que
- Si
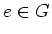 es el elemento identidad, entonces
es el elemento identidad, entonces 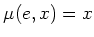 para todo
para todo 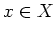 .
. - Si
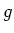 y
y 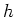 están en
están en 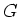 ,
entonces
,
entonces 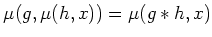 para todo
para todo 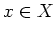 .
.
Ejercicio
1.13 (00) Probar que la aplicación ![]() es un homomorfismo de
grupos. Usar esto para redefinir la acción de un grupo sobre un conjunto.
es un homomorfismo de
grupos. Usar esto para redefinir la acción de un grupo sobre un conjunto.
Definición
1.5
Una acción ![]() de un grupo
de un grupo ![]() sobre un
conjunto
sobre un
conjunto ![]() , se dice transitiva, si siempre que
, se dice transitiva, si siempre que ![]() e
e ![]() están en
están en ![]() , existe un
elemento
, existe un
elemento ![]() tal
que
tal
que ![]() .
.
La siguiente construcción
nos permite dar todos los ejemplos de acciones de grupo transitivas: si ![]() es un grupo y
es un grupo y ![]() es un subgrupo, definimos la relación de
equivalencia
es un subgrupo, definimos la relación de
equivalencia ![]() si
si ![]() . El cociente
. El cociente ![]() es el
conjunto de clases a derecha sobre
es el
conjunto de clases a derecha sobre ![]() que también se denota
por
que también se denota
por ![]() .
.
Ejercicio
1.14 Probar que la acción ![]() definida por
definida por ![]() es transitiva.
es transitiva.
Definición
1.6
Sea ![]() una acción
transitiva de un grupo
una acción
transitiva de un grupo ![]() sobre un conjunto
sobre un conjunto ![]() . Si
. Si ![]() , definimos el subgrupo de isotropía de
, definimos el subgrupo de isotropía de ![]() ,
, ![]() como el conjunto de
todos los
como el conjunto de
todos los ![]() que fijan a
que fijan a ![]() (esto es,
(esto es, ![]() ).
).
Ejercicio
1.15 Sea ![]() una acción
transitiva de un grupo
una acción
transitiva de un grupo ![]() sobre un conjunto
sobre un conjunto ![]() y sea
y sea ![]() un elemento de
un elemento de ![]() . Encontrar
una biyección canónica entre
. Encontrar
una biyección canónica entre ![]() y
y ![]() .
.
Ejercicio
1.16 (00) Sea ![]() un espacio vectorial
real. Dar alguna acción transitiva de
un espacio vectorial
real. Dar alguna acción transitiva de ![]() sobre
sobre ![]() .
.
Ejercicio
1.17 (05) Si ![]() es el grupo de las
matrices
es el grupo de las
matrices ![]() ortogonales y
ortogonales y ![]() denota la esfera
unidad en
denota la esfera
unidad en ![]() , Entonces hay una acción natural
, Entonces hay una acción natural
![]()
definida por ![]() .
.
1.
Comprobar que es una
acción y probar que es transitiva.
2.
Identificar el subgrupo
de todas las transformaciones ortogonales que fijan "el Polo Norte" ![]() .
.
3.
Escribir la esfera como
un cociente de ![]() .
.
4.
* ¿Cuál es la dimensión
de ![]() ?
?
5.
* Demostrar que las
transformaciones ortogonales son los únicos elementos de ![]() que conservan las distancias.
que conservan las distancias.
A veces un
conjunto admite muchas acciones transitivas diferentes y se puede representar
de maneras diferentes como cociente de un grupo.
Ejercicio
1.18 (05) Consideremos la acción ![]() definida por
definida por ![]() . Demostrar que esta
acción es transitiva y escribir la esfera como un espacio de cociente de
. Demostrar que esta
acción es transitiva y escribir la esfera como un espacio de cociente de ![]() .
.
Ejercicio
1.19 *(20) Encontrar las acciones transitivas del
grupo unitario ![]() o el grupo especial unitario
o el grupo especial unitario ![]() sobre la
sobre la ![]() -esfera unidad y escribir
-esfera unidad y escribir ![]() como un espacio
cociente de
como un espacio
cociente de ![]() y de
y de ![]() . * Usar esto para
calcular la dimensión de
. * Usar esto para
calcular la dimensión de ![]() y de
y de ![]() .
.
Ejercicio
1.20 (15) El grupo euclídeo ![]() -dimensional
-dimensional ![]() es el conjunto
es el conjunto ![]() junto con el producto
junto con el producto ![]() .
.
1.
Comprobar que ![]() es un grupo.
es un grupo.
2.
Probar que la aplicación
![]() definida por
definida por ![]() (girar y luego trasladar), es una
acción transitiva.
(girar y luego trasladar), es una
acción transitiva.
3.
* Demostrar que las
transformaciones euclídeas son los únicos elementos de ![]() que conservan las distancias.
que conservan las distancias.
Ejercicio
1.21 (*20) El grupo ![]() -dimensional
afín
-dimensional
afín ![]() es el conjunto
es el conjunto ![]() junto con el producto
junto con el producto ![]() . Probar que
. Probar que ![]() actúa
transitivamente sobre el conjunto de elipses (o parábolas, o hipérbolas) sobre
el plano.
actúa
transitivamente sobre el conjunto de elipses (o parábolas, o hipérbolas) sobre
el plano.
Próximo:
Bibliografía Arriba: Grupos y sus acciones Anterior:
Ejemplos
importantes del álgebra