Próximo: Ejemplos
importantes del álgebra Arriba:
Grupos Anterior: Grupos
Motivación y definiciones básicas
Consideremos Biy![]() el conjunto de todas las biyecciones de un conjunto
el conjunto de todas las biyecciones de un conjunto ![]() en sí mismo. Si
en sí mismo. Si ![]() y
y ![]() son dos biyecciones, entonces también lo es su composición
son dos biyecciones, entonces también lo es su composición ![]() . Existe la biyección identidad que lleva cada elemento en sí
mismo, a la que llamamos
. Existe la biyección identidad que lleva cada elemento en sí
mismo, a la que llamamos ![]() , y tal que si
, y tal que si ![]() es cualquier
otra biyección, se tiene:
es cualquier
otra biyección, se tiene: ![]() . Además, cada biyección
. Además, cada biyección ![]() tiene una inversa
tiene una inversa ![]() , y la composición de una biyección y su inversa es igual a la
identidad.
, y la composición de una biyección y su inversa es igual a la
identidad.
Ejercicio 1.1 (05) Probar que la composición de biyecciones
es asociativa, pero no necesariamente conmutativa.
Ejercicio 1.2 (05) Cuando ![]() es el conjunto
es el conjunto ![]() , entonces Biy
, entonces Biy![]() es el
conjunto de las permutaciones de
es el
conjunto de las permutaciones de ![]() símbolos y se denota
por
símbolos y se denota
por ![]() . ¿Cuántos elementos hay en
. ¿Cuántos elementos hay en ![]() ?
?
*El código de César y la biblioteca de Borges. Si consideramos el conjunto de las biyecciones del
alfabeto ![]() , entramos en el mundo de la
criptografía. Ya en la antigüedad, Julio César la usó para cifrar sus mensajes
sustituyendo la letra
, entramos en el mundo de la
criptografía. Ya en la antigüedad, Julio César la usó para cifrar sus mensajes
sustituyendo la letra ![]() por la letra
por la letra ![]() , la
, la ![]() por la
por la ![]() , etcétera (la letra
, etcétera (la letra ![]() se sustituía por la
letra
se sustituía por la
letra ![]() ). El problema de este tipo de códigos es que ymjd fwj
jcywjrjqd jfxd yt gwjfp 1. Nota: También
puede leer “El escarabajo de oro” de Edgar Allan Poe.
). El problema de este tipo de códigos es que ymjd fwj
jcywjrjqd jfxd yt gwjfp 1. Nota: También
puede leer “El escarabajo de oro” de Edgar Allan Poe.
En un hermoso cuento titulado la Biblioteca de Babel,
Jorge Luis Borges describe una biblioteca de libros cuyas páginas están llenas
de las permutaciones de las letras del alfabeto, comas, puntos y espacios en
blanco. Desde luego, todo el conocimiento del Universo se podría encontrar en
una biblioteca de este estilo. Las páginas que ahora esta leyendo son también
de esta forma.
En el ejemplo de las biyecciones, tenemos un conjunto
junto con una operación (la composición) que dados dos elementos del conjunto y
le asigna otro. Además, esta operación satisface ciertas propiedades. Ya que
esta estructura aparece muy a menudo en matemáticas, es útil darle un nombre.
Definición
1.1
Un grupo está compuesto por un conjunto ![]() y una función
de multiplicación
y una función
de multiplicación
![]()
satisfaciendo
las siguientes propiedades:
- La multiplicación es asociativa:
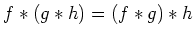 .
. - Existencia del elemento identidad: hay un elemento
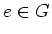 tal que para
cada
tal que para
cada 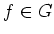 ,
,  .
. - Existencia de inverso: para cualquier elemento
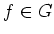 , hay otro elemento
, hay otro elemento 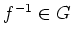 tal que
tal que  .
.
Definición
1.2
Sea ![]() un grupo y
un grupo y ![]() un subconjunto de
un subconjunto de ![]() . Decimos que
. Decimos que ![]() es un subgrupo de
es un subgrupo de ![]() si
si
- La identidad pertenece a
 .
. - Siempre que un elemento está en
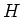 también está su inverso.
también está su inverso. - Siempre que dos elementos están en
 también está su producto.
también está su producto.
Claramente, si ![]() es un subgrupo de
es un subgrupo de ![]() , entonces
, entonces ![]() es un grupo.
es un grupo.
Ejercicio 1.3 (*10) ¿Cual es la probabilidad de que un
subconjunto de ![]() sea un subgrupo?
sea un subgrupo?
(1) En la traducción se ha dejado el texto cifrado en el
idioma original (inglés). Una traducción al castellano podría ser:
xts wjfqrjsyj
kfhnqjx ij wtrujw.
Próximo:
Ejemplos
importantes del álgebra Arriba: Grupos Anterior: Grupos