Siguiente: Ecuaciones
de las Variedades Subir:
Espacio afín Anterior: Aplicaciones Afines.
Espacios Afines de Dimensión Finita.
Definición 3.1 Sea ![]() . Se llama sistema de referencia
cartesiano o afín de
. Se llama sistema de referencia
cartesiano o afín de ![]() a todo par
a todo par ![]() donde
donde ![]() y
y ![]() es una base de
es una base de ![]() .
.
Definición 3.2 Dado un sistema de
referencia ![]() y dado
y dado ![]() , tenemos
, tenemos ![]() y por tanto
y por tanto ![]() . A
. A ![]() se le llaman coordenadas cartesianas o
afines del punto
se le llaman coordenadas cartesianas o
afines del punto ![]() respecto del sistema de referencia
respecto del sistema de referencia ![]() .
.
Ejercicio 3.3 (Cambio de sistema de
referencia cartesiano).
Sean ![]() y
y ![]() dos sistemas de referencias cartesianas
y sean
dos sistemas de referencias cartesianas
y sean ![]() las coordenadas de un punto
las coordenadas de un punto ![]() respecto de ambos sistemas de referencia. Probar que se tiene
la siguiente igualdad:
respecto de ambos sistemas de referencia. Probar que se tiene
la siguiente igualdad:
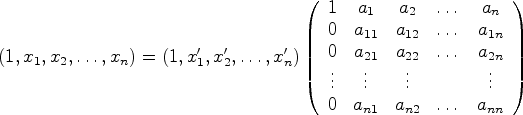
Donde ![]() son las coordenadas de
son las coordenadas de ![]() en el sistema de referencia
en el sistema de referencia ![]() y
y ![]() .
.
Definición 3.4 Sean ![]()
![]() puntos de
puntos de ![]() . Se dice que son afinmente
independientes si los vectores
. Se dice que son afinmente
independientes si los vectores ![]() ,
, ![]() , ... ,
, ... , ![]() son linealmente independientes.
son linealmente independientes.
Ejercicio 3.5 Probar que por ![]() puntos afinmente
independientes,
puntos afinmente
independientes, ![]() , pasa una única variedad
, pasa una única variedad ![]() de dimensión
de dimensión ![]() . Definida por:
. Definida por: ![]() .
.
Siguiente: Ecuaciones de las Variedades Subir: Espacio afín Anterior: Aplicaciones Afines.
David Llena Carrasco 2003-10-31