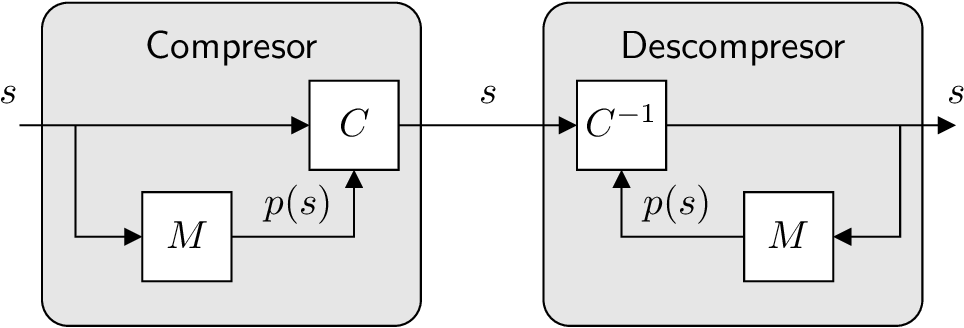
Figure 1: Block diagram of the entropy encoding/decoding.
| (Eq:symbol_information) |
bits of information.
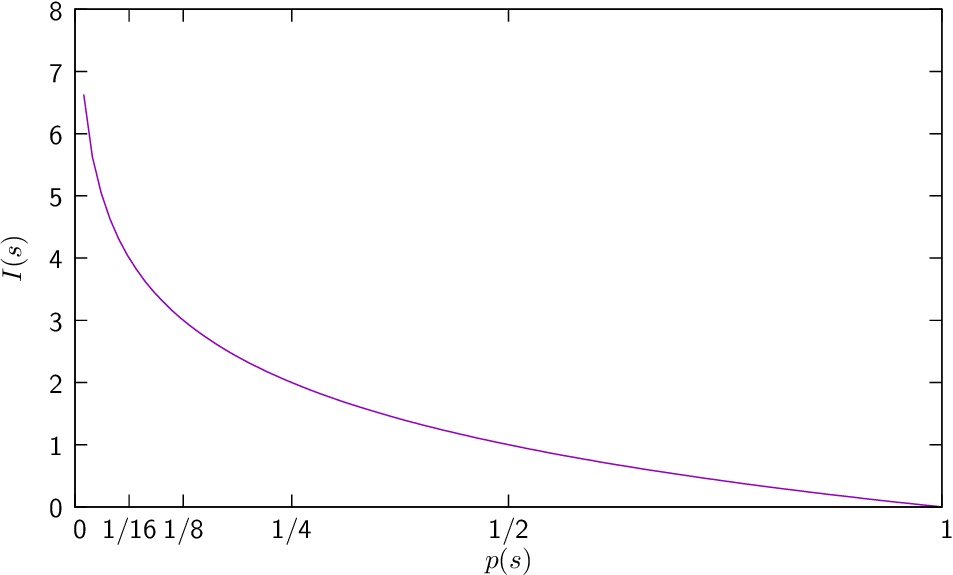
| (1) |
bits-of-information/symbol, where is the size of the source alphabet (number of different symbols).