Contents

1 Fundamentals

• S.W. Golomb designs in 1966 an alternative to the Huffman coding [1].
• When the probabilities of the symbols follow an exponential distribution, the Golomg encoder has the same efficiency than the Huffman coding, but it is faster. In this case, the probabilities of the symbols shoud be

  $$p\left(s\right)=2^{-\left(\right.m⌊\frac{s+m}{m}⌋\left)\right.}$$

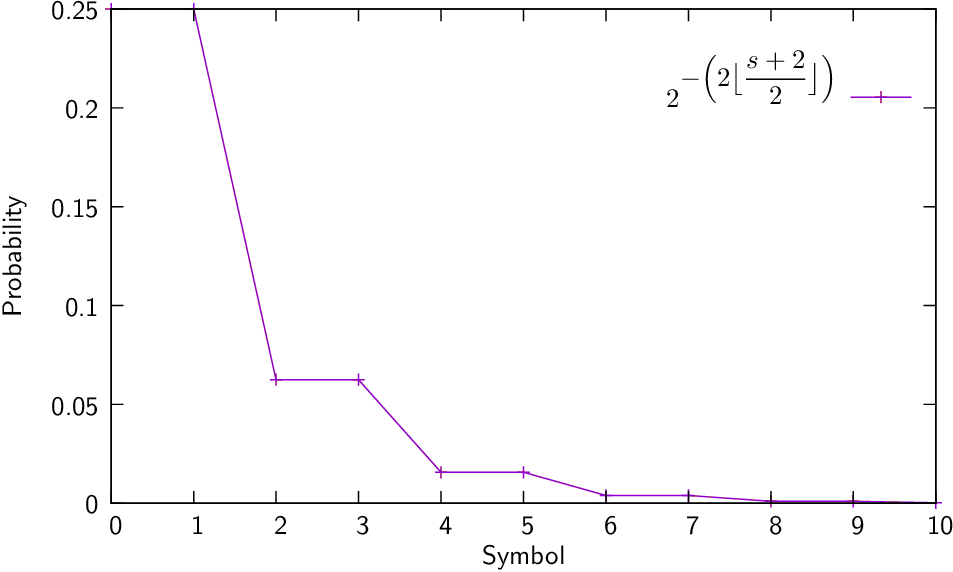
  (Eq:Golomb)

  where $s=0,1,\cdots$ is the symbol and $m=0,1,\cdots$ is the “Golomb slope” of the distribution.

• For $m=2^k$, it is possible to find a very efficient implementation and the encoder is also named Rice encoder [2]. In this case

  $$p\left(s\right)=2^{-\left(\right.2^k⌊\frac{s+2^k}{2^k}⌋\left)\right.}$$

  (Eq:Rice)

• Notice that for $m=1$, we take the unary encoding.

2 The Golomb encoder

1. $k\leftarrow \lceil {log}_2\left(m\right)\rceil$.
2. $r\leftarrow s\mathrm{mod}m$.
3. $t\leftarrow 2^k-m$.
4. Output $\left(s\mathrm{div}m\right)$ using an unary code.
5. If $r<t$:
   1. Output the integer encoded in the $k-1$ least significant bits of $r$ using a binary code.
6. Else:
   1. $r\leftarrow r+t$.
   2. Output the integer encoded in the $k$ least significant bits of $r$ using a binary code.

Example ($m=7$ and $s=8$)

1. $k\leftarrow \lceil {log}_2\left(8\right)\rceil =3$.
2. $r\leftarrow 8\text{mod}7=1$.
3. $t\leftarrow 2^3-7=8-7=1$.
4. Output $\leftarrow 8\text{div}7=\lfloor 8∕7\rfloor =1$ as an unary code (2 bits).
   Therefore, output $\leftarrow 10$.
5. $r=1\le t=1$.
6. $r\leftarrow 1+1=2$.
7. Output $r=2$ using a binary code of $k=3$ bits.
   Therefore, $c\left(8\right)=10010$.

3 The Golomb decoder

1. $k\leftarrow \lceil {log}_2\left(m\right)\rceil$.
2. $t\leftarrow 2^k-m$.
3. Let $s\leftarrow$ the number of consecutive ones in the input (we stop when we read a $0$).
4. Let $x\leftarrow$ the next $k-1$ bits in the input.
5. If $x<t$:
   1. $s\leftarrow s\times m+x$.
6. Else:
   1. $x\leftarrow x\times 2+$ next input bit.
   2. $s\leftarrow s\times m+x-t$.

Example (decode $10010$ where $m=7$)

1. $k\leftarrow 3$.
2. $t\leftarrow 2^k-m=2^3-7=1$).
3. $s\leftarrow 1$ because we found only one $1$ in the input.
4. $x\leftarrow {\text{input}}_{k-1}={\text{input}}_2=01$.
5. $x=1\nless t=1$.
6. $x\leftarrow x\times x\times 2+\text{next input bit}=x\times 1\times 2+0=2$.
7. $s\leftarrow s\times m+x-t=1\times 7+2-1=8$.

Let’s go the the lab!

1. make golomb.
2.                     Codec | lena boats pepers zelda Average  
   --------------------------+--------------------------------  
                           : |    :     :      :     :       :  
                      golomb | ....  ....   ....  ....    ....  
              tpt 1 | golomb | ....  ....   ....  ....    ....

   Note: this implementation of the Golomb encoding estimates the $m$ parameter automatically.

4 The Rice encoder

1. $m\leftarrow 2^k$.
2. Output $\leftarrow \lfloor s∕m\rfloor$ using an unary code ($\lfloor s∕m\rfloor +1$ bits).
3. Output $\leftarrow$ the $k$ least significant bits of $s$ using a binary code.

Example ($k=1$ and $s=7$)

1. $m\leftarrow 2^k=2^1=2$.
2. Output $\leftarrow \lfloor s∕m\rfloor =\lfloor 7∕2\rfloor =3$ using an unary code of 4 bits. Therefore, output $\leftarrow 1110$.
3. Output $\leftarrow$ the $k=1$ least significant bits of $s=7$ using a unary code ($k+1$ bits). So, output $\leftarrow 1$. Total output $c\left(7\right)=11101$.

5 The Rice decoder

1. Let $s$ the number of consecutive ones in the input (we stop when we read a 0).
2. Let $x$ the next $k$ input bits.
3. $s\leftarrow s\times 2^k+x$.

Example (decode $11101$ where $k=1$)

1. $s\leftarrow 3$ because we found $3$ consecutive ones in the input.
2. $x\leftarrow$ next input $k=1$ input bits. Therefore $x\leftarrow 1$.
3. $s\leftarrow s\times 2^k+x=3\times 2^1+1=6+1=7$.

Let’s go the the lab!

1. make rice.
2.                     Codec | lena boats pepers zelda Average  
   --------------------------+--------------------------------  
                           : |    :     :      :     :       :  
                        rice | ....  ....   ....  ....    ....  
                tpt 1 | rice | ....  ....   ....  ....    ....

   Note: this implementation of the Rice encoding estimates the $k$ parameter automatically.

References