Siguiente: Sobre este documento... Subir: Estudio afín y euclídeo Anterior: Clasificación proyectiva y afín

Haces de hipercuádricas

Como sabemos las hipercuádricas proyectivas se obtienen como proyectivización de las formas cuadráticas sobre el espacio vectorial correspondiente y éstas son equivalentes a las formas bilineales que como sabemos de la geometría elemental, forman un espacio vectorial de dimensión $\frac{n(n+1)}{2}$, donde $n$ es la dimensión del espacio vectorial en cuestión.

Dicho de otra forma, podemos considerar las hipercuádricas de $P(V)$ como puntos del espacio proyectivo $P(S_2(V))$, donde $S_2(V)$ es el espacio vectorial de las formas bilineales simétricas sobre $V$.

Ejercicio 5.1   Dado $M$ un punto de $P(V)$ entonces

 

$$C(M)=\{\mathcal{Q}\in P(S_2(V))\colon M\in\mathcal{Q}\}$$

 

es un hiperplano proyectivo de $P(S_2(V))$.

El conjunto anterior está formado por todas las cónicas que pasan por $M$, si aumentamos el número de puntos hasta que coincida con $\frac{n(n+3)}{2}$ (la dimensión de $P(S_2(V))$), podemos concluir que dados $\frac{n(n+3)}{2}$ puntos de un espacio proyectivo $P(V)$, siempre existe al menos una cónica que pasa por ellos. Esto es una generalización del resultado que vimos en el apartado cuatro del tema anterior.

Definición 5.2   Se llama haz de hipercuádricas en $P(V)$ a una recta proyectiva de $P(S_2(V))$ Dicho de otra manera a una ecuación de la forma:

$$Q+\lambda Q'=0$$

donde $Q$, $Q'$ son formas cuadráticas sobre $V$ y $\lambda\in k$.

A partir de la ecuación anterior, y dadas $\mathcal{Q}$, $\mathcal{Q}'$ hipercuádricas asociadas, los puntos de corte de $\mathcal{Q}$ y $\mathcal{Q}'$ son puntos pertenecientes a todas las hipercuádricas del haz, o equivalentemente estos puntos determinan el haz.

Nuestro objetivo es, en el caso de las cónicas, fijar este número de puntos necesarios para determinar el haz y dar un método para generar todas las cónicas de dicho haz.

La idea es bastante sencilla, basta con encontrar dos cónicas del haz, y a partir de ellas generar todas las demás.

Vamos a buscar las cónicas más sencillas, en este caso serán degeneradas y formadas por un par de rectas no necesariamente distintas.

Ejercicio 5.3   Probar que, en el caso de cónicas, el corte de dos de ellas son cuatro puntos (no necesariamente distintos), o un número infinito de puntos. Determinar cuales son los casos en esta segunda posibilidad. Los cuatro puntos del primer caso los llamaremos puntos fijos del haz.

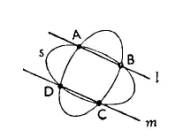
Ejercicio 5.4   Clasificar los haces de cónicas según los puntos fijos. Y determinar el número de cónicas degeneradas en los siguientes casos:

1.    Cuatro puntos fijos distintos.

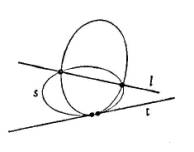
2.    Dos puntos fijos confundidos y dos distintos.

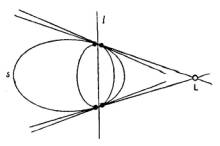
3.    Dos parejas de puntos fijos confundidos.

4.    Tres puntos fijos confundidos y uno distinto.

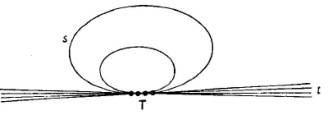
5.    Cuatro puntos fijos confundidos.

Ejercicio 5.5   Sean $A$, $B$, $C$ y $D$ los cuatro puntos fijos distintos de un haz de cónicas. Probar que los tres puntos diagonales del cuadrivértice $ABCD$ son autopolares respecto a todas las cónicas del haz.

Terminamos este apartado proponiendo la demostración de un teorema debido a Desargues.

Ejercicio 5.6   Los pares de puntos en los que una recta fija corta a las cónicas de un haz, son pares en involución.

Siguiente: Sobre este documento... Subir: Estudio afín y euclídeo Anterior: Clasificación proyectiva y afín