Siguiente: Estudio Afín Subir:
Estudio afín y euclídeo Anterior: Estudio afín y euclídeo
Algunas definiciones
Siguiendo la misma
notación que en el ejercicio 2.4 del capítulo anterior, donde ![]() es la forma cuadrática asociada a una
forma bilineal
es la forma cuadrática asociada a una
forma bilineal ![]() podemos
hacer las siguientes definiciones:
podemos
hacer las siguientes definiciones:
Definición
1.1
Dos vectores ![]() y
y ![]() se dicen conjugados respecto a
se dicen conjugados respecto a ![]() si
si ![]() , donde
, donde ![]() es la forma
bilineal (simétrica) asociada a
es la forma
bilineal (simétrica) asociada a ![]() .
.
Definición
1.2
Si ![]() es un conjunto de vectores de
es un conjunto de vectores de ![]() , llamaremos
, llamaremos ![]() al conjunto de todos
los vectores de
al conjunto de todos
los vectores de ![]() que son conjugados con todos los de
que son conjugados con todos los de ![]() respecto de la forma cuadrática
respecto de la forma cuadrática ![]()
![]()
Ejercicio 1.3 (00) Probar que ![]() .
.
Definición
1.4
Un vector se dice autoconjugado respecto a ![]() si
si ![]() .
.
A partir de las
definición anterior, vemos que los puntos de la hipercuádrica ![]() corresponden a los “puntos” autoconjugados de
la forma cuadrática asociada.
corresponden a los “puntos” autoconjugados de
la forma cuadrática asociada.
Esta relación es muy útil para trabajar con las
hipercuádricas y la llamaremos polaridad
Definición
1.5
Sea ![]() la hipercuádrica proyectiva asociada a
una forma cuadrática
la hipercuádrica proyectiva asociada a
una forma cuadrática ![]() .
Se define la polaridad asociada a
.
Se define la polaridad asociada a ![]() ,
como la aplicación proyectiva inducida por la aplicación:
,
como la aplicación proyectiva inducida por la aplicación:
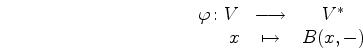
donde ![]() es la forma bilinear simétrica asociada
a
es la forma bilinear simétrica asociada
a ![]() .
.
Desde esta definición, el
subespacio polar de ![]() respecto de la hipercuádrica proyectiva
respecto de la hipercuádrica proyectiva ![]() sería el conjunto
sería el conjunto ![]() ,
donde
,
donde ![]() es el conjugado de
es el conjugado de ![]() respecto de
respecto de ![]() ,
la forma cuadrática asociada a
,
la forma cuadrática asociada a ![]() .
.
En el caso del plano proyectivo si ![]() es una cónica, el subespacio polar de
una recta respecto a
es una cónica, el subespacio polar de
una recta respecto a ![]() es un punto llamado polo de la recta y el subespacio polar de
un punto es una recta que se llama recta polar del punto.
es un punto llamado polo de la recta y el subespacio polar de
un punto es una recta que se llama recta polar del punto.
Definición
1.6
Se dice que dos rectas son conjugadas si cada una de ellas contiene al
polo de la otra.
Ejercicio 1.7 (00) Probar que la correspondencia polo-polar
es biunívoca, es decir, el polo de la polar de un punto es el propio punto y
análogamente la polar del polo de una recta es la propia recta.
Ejercicio 1.8 (-05) Probar que las rectas tangentes a la
cónica son aquellas que contienen a su polo.
Siguiente:
Estudio
Afín Subir: Estudio afín y euclídeo Anterior:
Estudio
afín y euclídeo