Próximo: Bibliografía Arriba:
Geometría de la Recta Anterior: La recta proyectiva compleja
La acción de 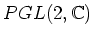 sobre
sobre 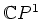
Desde el punto
de vista algebraico, hay poca diferencia entre la descripción de la acción del
grupo complejo proyectivo sobre el espacio proyectivo complejo y la descripción
de la acción del grupo proyectivo real sobre el espacio proyectivo real.
Ejercicio 2.1 (00) Probar que la acción de ![]() sobre
sobre ![]() definida por
definida por ![]() es transitiva. Demostrar que una matriz
es transitiva. Demostrar que una matriz ![]() fija todos los puntos de
fija todos los puntos de ![]() si y sólo si es un múltiplo de la
identidad.
si y sólo si es un múltiplo de la
identidad.
Definición
2.1
El grupo proyectivo ![]() ,
, ![]() es el cociente de
es el cociente de ![]() por la relación de equivalencia: dos matrices son
equivalentes si son múltiplo la una de la otra.
por la relación de equivalencia: dos matrices son
equivalentes si son múltiplo la una de la otra.
Ejercicio
2.2 (00) Usar el ejercicio 2.1 para definir una
acción transitiva de ![]() sobre
sobre ![]() . Mostrar que si un elemento del grupo
proyectivo fija todos los puntos en el espacio proyectivo, entonces es la
identidad.
. Mostrar que si un elemento del grupo
proyectivo fija todos los puntos en el espacio proyectivo, entonces es la
identidad.
Ejercicio 2.3 Identificamos ![]() con
con ![]() más el punto del infinito y consideramos
más el punto del infinito y consideramos
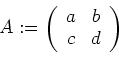
una matriz invertible (compleja). Demostrar el efecto
de la acción de ![]() sobre un número complejo
sobre un número complejo ![]() es igual a
es igual a ![]() .
.
Las transformaciones de la forma ![]() se llaman normalmente transformaciones
de Moebius o transformaciones lineales fraccionarias.
se llaman normalmente transformaciones
de Moebius o transformaciones lineales fraccionarias.
Ejercicio 2.4 (00) Utilizando las fórmulas del capítulo 2,
es fácil ampliar los teoremas fundamentales (primero y segundo) de la geometría
proyectiva al caso complejo.
1.
Probar que existe una
transformación única de la forma
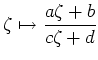
que lleva una
terna de números complejos distintos ![]() a
a ![]() .
.
2.
Escribir la fórmula para
la transformación proyectiva que lleva ![]() a
a
![]() (esto es, la inversa de la transformación
anterior).
(esto es, la inversa de la transformación
anterior).
3.
Escribir la fórmula para
la transformación que lleva ![]() a
a ![]() .
.
Como
consecuencia trivial de este ejercicio tenemos:
Teorema
2.2 (Primer teorema fundamental) Si ![]() y
y ![]() son dos ternas de puntos distintos sobre la recta proyectiva
compleja, existe una única transformación proyectiva que envía
son dos ternas de puntos distintos sobre la recta proyectiva
compleja, existe una única transformación proyectiva que envía ![]() a
a ![]() ,
, ![]() a
a ![]() y
y ![]() a
a ![]() .
.
Definición 2.3 Sea ![]() una cuaterna de puntos sobre la recta proyectiva compleja con
una cuaterna de puntos sobre la recta proyectiva compleja con
![]() ,
, ![]() y
y ![]() diferentes unos de otros, y sea
diferentes unos de otros, y sea ![]() la única
transformación proyectiva que lleva
la única
transformación proyectiva que lleva ![]() ,
, ![]() y
y ![]() respectivamente sobre
respectivamente sobre ![]() , 0 y
, 0 y ![]() . La razón doble
. La razón doble ![]() se define como el punto
se define como el punto ![]() .
.
Ejercicio 2.5 (00) Identificando la recta proyectiva
compleja con ![]() , comprobar que la razón doble
de cuatro números complejos
, comprobar que la razón doble
de cuatro números complejos ![]() se puede escribir como:
se puede escribir como:
![$\displaystyle [z_0,z_1,z_2,z_3]=\frac{z_2-z_0}{z_2-z_1}\frac{z_3-z_1}{z_3-z_0}
$](img67.png)
Ejercicio 2.6 (00) Probar que si ![]() es una
transformación proyectiva y
es una
transformación proyectiva y ![]() es una cuaterna de puntos sobre la recta
proyectiva con
es una cuaterna de puntos sobre la recta
proyectiva con ![]() ,
, ![]() y
y
![]() diferentes unos de otros, entonces la razón doble
diferentes unos de otros, entonces la razón doble ![]() es igual a
es igual a ![]() .
.
Teorema 2.4 (Segundo teorema fundamental) Una
transformación de la recta proyectiva compleja en sí misma es una
transformación proyectiva si y sólo si conserva las razones dobles.
Ejercicio 2.7 (00) Demostrar el teorema 2.2.
Los ejercicios
precedentes - copias exactas de los del capítulo 2 - pueden llevar al lector a creer
que la geometría de la recta proyectiva compleja es similar a la de la recta
proyectiva real. En este momento veremos que el caso complejo es infinitamente
más rico y más hermoso. En primer lugar, las circunferencias juegan un papel
privilegiado en la geometría proyectiva compleja.
Observación. De ahora en adelante llamaremos rectas tanto a las
rectas como a las circunferencias. La idea intuitiva consiste en que una recta
es un circunferencia de radio infinito, o simplemente la proyección estereográfica
de un circunferencia que pasa por el Polo Norte.
Ejercicio
2.8 (10) Probar que cuatro puntos en ![]() están sobre la misma circunferencia si y sólo si su razón
doble es un número real.
están sobre la misma circunferencia si y sólo si su razón
doble es un número real.
Ejercicio 2.9 (05) Escribir la ecuación de la circunferencia
que pasa por los puntos ![]() ,
, ![]() y
y ![]() .
.
Una consecuencia
obvia de ejercicio 2.8 es el siguiente resultado importante.
Proposición
2.5
Las transformaciones de Moebius llevan circunferencias a circunferencias.
Ejercicio
2.10 (10) Demostrar que dadas dos circunferencias
cualesquiera existe siempre una transformación de Moebius que lleva una
circunferencia en la otra.
Para entender
mejor las transformaciones de Moebius, consideraremos tres casos particulares.
Los dos primeros son ya familiares: las transformaciones de la forma ![]() son las traslaciones del número
son las traslaciones del número ![]() pensado como un vector sobre el plano,
las transformaciones de la forma
pensado como un vector sobre el plano,
las transformaciones de la forma ![]() ,
, ![]() son dilataciones (homotecias) compuestas
con rotaciones alrededor del origen. El tercer caso, la inversión
son dilataciones (homotecias) compuestas
con rotaciones alrededor del origen. El tercer caso, la inversión ![]() , es más interesante.
, es más interesante.
Ejercicio
2.11 (15) Sea ![]() un punto sobre
un punto sobre ![]() y sea
y sea ![]() la imagen inversa de
la imagen inversa de ![]() por la proyección
estereográfica desde el Polo Norte de la esfera unidad. Tracemos una recta
desde
por la proyección
estereográfica desde el Polo Norte de la esfera unidad. Tracemos una recta
desde ![]() al
Polo Sur y consideremos el punto donde esta recta corta a
al
Polo Sur y consideremos el punto donde esta recta corta a ![]() . Demostrar que este punto es
. Demostrar que este punto es ![]() .
.
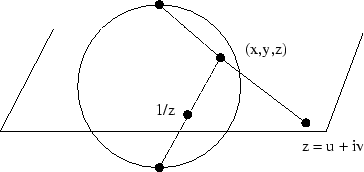
El lector debe tener presente que las transformaciones
de Moebius son transformaciones proyectivas complejas solamente cuando se ven
en el modelo que identifica ![]() con
con ![]() más el punto del infinito. El cambio de este
modelo por la esfera, conduce a nuevas ideas como la que hemos presentado en el
ejercicio anterior. Otro ejemplo viene dado en el siguiente ejercicio:
más el punto del infinito. El cambio de este
modelo por la esfera, conduce a nuevas ideas como la que hemos presentado en el
ejercicio anterior. Otro ejemplo viene dado en el siguiente ejercicio:
Ejercicio
2.12 2.12 (*15) Probar que una transformación de
Moebius ![]() induce una rotación sobre la esfera
si y sólo si
induce una rotación sobre la esfera
si y sólo si ![]() y
y ![]() . En otras palabras si y sólo si la matriz
. En otras palabras si y sólo si la matriz
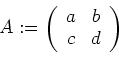
es unitaria.
Pista: Las rotaciones fijan un par de puntos antípodas.
Como podemos multiplicar todas las entradas de ![]() por el mismo número
no nulo complejo sin cambiar la transformación, podemos asumir que el
determinante de
por el mismo número
no nulo complejo sin cambiar la transformación, podemos asumir que el
determinante de ![]() es igual a 1. Usar esto para identificar el grupo
es igual a 1. Usar esto para identificar el grupo ![]() con el doble recubridor del grupo de rotaciones
con el doble recubridor del grupo de rotaciones ![]() .
.
Ejercicio
2.13 (20) Probar que cualquier transformación de
Moebius es la composición de translaciones, homotecias, rotaciones e
inversiones.
Ejercicio
2.14 (10) El resultado anterior nos permite dar una
nueva prueba de que las circunferencias se conservan mediante transformaciones
de Moebius. De hecho, esto basta para demostrar que la inversión ![]() envía circunferencias a circunferencias.
envía circunferencias a circunferencias.
- Sean
 y
y  números reales y sea
números reales y sea 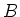 un número
complejo. Demostrar que la ecuación
un número
complejo. Demostrar que la ecuación 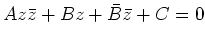 define un circunferencia si y sólo
si
define un circunferencia si y sólo
si 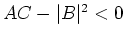 . Recíprocamente, demostrar
que cualquier circunferencia tiene una ecuación de esta forma.
. Recíprocamente, demostrar
que cualquier circunferencia tiene una ecuación de esta forma. - Usando lo anterior demostrar que las transformaciones de Moebius
llevan circunferencias a circunferencias.
- Una anti-homografía es una transformación de la forma
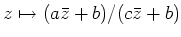 , con
, con 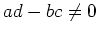 . Demostrar que las anti-homografías
también envían circunferencias a circunferencias.
. Demostrar que las anti-homografías
también envían circunferencias a circunferencias.
Además de llevar
circunferencias a circunferencias, las transformaciones de Moebius tienen
importante la propiedad de conservar los ángulos y la orientación. Para verlo
en el contexto apropiado, estudiaremos todas las transformaciones que
satisfacen esta propiedad.
Ejercicio
2.15 (20) Demostrar que la transformación lineal de
![]() en sí mismo definida por la matriz
invertible
en sí mismo definida por la matriz
invertible
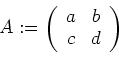
Conserva los
ángulos y la orientación si y sólo si ![]() y
y ![]() . En otras palabras,
. En otras palabras,
![]() representa la
multiplicación por un número complejo no nulo . Pista:
representa la
multiplicación por un número complejo no nulo . Pista: ![]() conserva la orientación si y sólo si su
determinante es positivo.
conserva la orientación si y sólo si su
determinante es positivo.
Definición
2.6
Una aplicación diferenciable de un abierto de ![]() en
en ![]() se dice que conserva ángulos si en
cada punto la diferencial
se dice que conserva ángulos si en
cada punto la diferencial
![]()
es una
transformación lineal que conserva ángulos. De la misma manera, se dice que ![]() conserva la orientación si su diferencial es una aplicación
lineal que conserva la orientación.
conserva la orientación si su diferencial es una aplicación
lineal que conserva la orientación.
Una aplicación diferenciable desde un subconjunto
abierto de ![]() en
en ![]() que conserva ángulos y orientaciones se dice conforme.
que conserva ángulos y orientaciones se dice conforme.
Ejercicio
2.16 (10) Este ejercicio muestra que las
aplicaciones conformes se caracterizan por un sistema simple de ecuaciones
diferenciales.
1.
Probar que una
aplicación diferenciable ![]() de un subconjunto abierto de
de un subconjunto abierto de ![]() en
en ![]() es conforme si y sólo si cumple las
ecuaciones de Cauchy-Riemann:
es conforme si y sólo si cumple las
ecuaciones de Cauchy-Riemann:
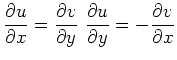
2.
Sea ![]() . Probar que
. Probar que ![]() es conforme si y sólo si
es conforme si y sólo si ![]() es idénticamente igual a cero.
es idénticamente igual a cero.
3.
Probar que si ![]() es una transformación
conforme, entonces
es una transformación
conforme, entonces ![]() y
y ![]() son funciones armónicas, es decir:
son funciones armónicas, es decir:
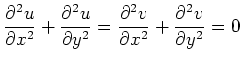
Ejercicio
2.17 (10) Sean ![]() y
y ![]() dos
aplicaciones conformes definidas sobre algún subconjunto abierto de
dos
aplicaciones conformes definidas sobre algún subconjunto abierto de ![]() . En este ejercicio, consideraremos que los
valores de
. En este ejercicio, consideraremos que los
valores de ![]() y
y ![]() son números complejos en lugar de verlos
solamente como puntos o vectores en
son números complejos en lugar de verlos
solamente como puntos o vectores en ![]() .
.
1.
Probar que la aplicación
![]() es conforme.
es conforme.
2.
Probar que la aplicación
![]() (la
multiplicación compleja) es conforme. Concluir que cualquier polinomio complejo
define una aplicación conforme.
(la
multiplicación compleja) es conforme. Concluir que cualquier polinomio complejo
define una aplicación conforme.
3.
Supongamos que ![]() no es idénticamente nula. Probar que la función
no es idénticamente nula. Probar que la función ![]() es conforme sobre su dominio de
definición. Concluir que una función racional (esto es, un cociente de dos
polinomios) es conforme sobre su dominio de definición.
es conforme sobre su dominio de
definición. Concluir que una función racional (esto es, un cociente de dos
polinomios) es conforme sobre su dominio de definición.
El ejercicio
anterior demuestra el siguiente resultado importante:
Teorema 2.7 Las transformaciones de Moebius son
aplicaciones conformes.
Usando que las
transformaciones de Moebius conservan ángulos, podemos dar una prueba simple de
que la proyección estereográfica conserva ángulos.
Ejercicio
2.18 Usar el ejercicio 1.7, el teorema anterior y el hecho de que las rotaciones
sobre la esfera se pueden representar por transformaciones de Moebius para
demostrar que la proyección estereográfica conserva ángulos.
Próximo:
Bibliografía Arriba: Geometría de la Recta Anterior:
La recta
proyectiva compleja