Próximo: La acción
de sobre Arriba:
Geometría de la Recta Anterior: Geometría de la Recta
La recta proyectiva compleja
Definición 1.1 El espacio proyectivo complejo ![]() -dimensional
-dimensional ![]() es el conjunto de todas las rectas complejas sobre
es el conjunto de todas las rectas complejas sobre ![]() que pasan por el origen.
que pasan por el origen.
Nótese que
también podemos definir ![]() como el cociente de
como el cociente de ![]() por la relación de equivalencia
por la relación de equivalencia ![]() si
si ![]() y
y ![]() son múltiplos complejos el uno del otro.
son múltiplos complejos el uno del otro.
Si ![]() es un vector no nulo de
es un vector no nulo de ![]() expresado en la base canónica, denotamos
su clase de equivalencia por
expresado en la base canónica, denotamos
su clase de equivalencia por ![]() .
.
Como ![]() es un espacio vectorial de dimensión cuatro
sobre los reales, parece difícil a primera vista tener una idea intuitiva de la
recta proyectiva compleja. Los ejercicios siguientes muestran que la recta
proyectiva compleja puede ser como la recta compleja
es un espacio vectorial de dimensión cuatro
sobre los reales, parece difícil a primera vista tener una idea intuitiva de la
recta proyectiva compleja. Los ejercicios siguientes muestran que la recta
proyectiva compleja puede ser como la recta compleja ![]() más un punto en el infinito o como la esfera
unidad en
más un punto en el infinito o como la esfera
unidad en ![]() .
.
Ejercicio 1.1 (00) Probar que la aplicación de ![]() en
en ![]() definida por
definida por
![]()
Es una biyección.
Ejercicio 1.2 (10) Sea ![]() la aplicación que lleva los vectores no
nulos de
la aplicación que lleva los vectores no
nulos de ![]() a vectores en
a vectores en ![]() según la regla siguiente:
según la regla siguiente:
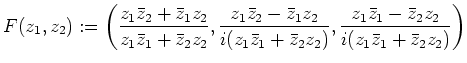
Probar que ![]() define una biyección
entre
define una biyección
entre ![]() y la esfera unidad en
y la esfera unidad en ![]() .
.
La proyección
estereográfica da la relación entre ambas representaciones de la recta
proyectiva compleja.
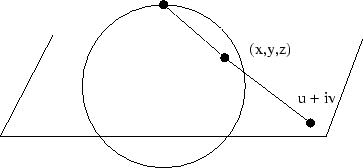
Ejercicio 1.3 (10) Sea ![]() un punto sobre
un punto sobre ![]() distinto del Polo Norte
distinto del Polo Norte ![]() . Probar que la recta que une
. Probar que la recta que une ![]() con el Polo Norte corta al plano
con el Polo Norte corta al plano ![]() en el punto
en el punto ![]() .
.
Definición 1.2 La proyección estereográfica es la
aplicación ![]() definida por
definida por
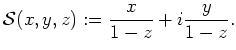
Ejercicio 1.4 (05) Probar que la inversa de la proyección
estereográfica lleva un número complejo ![]() al punto
al punto
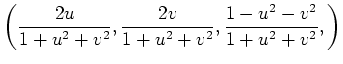
sobre la esfera
unidad.
Un lector agudo
debe haber notado la semejanza entre la fórmula precedente y la del ejercicio
1.2. El ejercicio siguiente da la relación exacta:
Ejercicio 1.5 (05) Sea ![]() un punto sobre
un punto sobre ![]() diferente de
diferente de ![]() . Probar que
. Probar que ![]() .
.
La existencia de
estos dos modelos geométricos para ![]() y sus conexiones con los números complejos y la geometría
espacial es central para el entendimiento de la geometría de la recta
proyectiva compleja. Para pasar de un modelo a otro, tenemos que entender bien
las propiedades de la proyección estereográfica.
y sus conexiones con los números complejos y la geometría
espacial es central para el entendimiento de la geometría de la recta
proyectiva compleja. Para pasar de un modelo a otro, tenemos que entender bien
las propiedades de la proyección estereográfica.
Ejercicio 1.6 (20) Probar que la imagen de una
circunferencia sobre ![]() mediante la proyección estereográfica es o una circunferencia
o una recta. Además, la imagen de una circunferencia es una recta si y sólo si
la circunferencia pasa por el Polo Norte.
mediante la proyección estereográfica es o una circunferencia
o una recta. Además, la imagen de una circunferencia es una recta si y sólo si
la circunferencia pasa por el Polo Norte.
Otra propiedad
importante de la proyección estereográfica es que conserva ángulos. Daremos una
prueba simple de este hecho más tarde, pero invitamos al lector a verificar
esta propiedad en el caso más simple posible:
Ejercicio
1.7 (05) Probar que la imagen por la proyección
estereográfica de dos curvas sobre ![]() que se cortan en el polo sur con un
ángulo
que se cortan en el polo sur con un
ángulo ![]() consiste en dos curvas sobre el plano que se cortan en el
origen con un ángulo
consiste en dos curvas sobre el plano que se cortan en el
origen con un ángulo ![]() .
.
Próximo:
La acción
de sobre Arriba: Geometría de la Recta Anterior:
Geometría
de la Recta