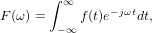 | (1) |
donde e−jωt es la funci’on exponencial compleja. La funci’on F(ω) representa las amplitudes de las infinitas componentes espectrales de f(t) y se conoce como funci’on de densidad espectral.
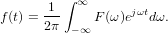 | (2) |
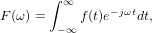 | (1) |
donde e−jωt es la funci’on exponencial compleja. La funci’on F(ω) representa las amplitudes de las infinitas componentes espectrales de f(t) y se conoce como funci’on de densidad espectral.
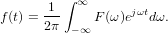 | (2) |
![F[f(t)] = F (ω ),](index2x.png)
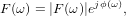
 | (3) |
y donde ϕ(ω) es el argumento o fase de F(ω) y se calcula como
 | (4) |
siendo
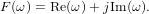 | (5) |
Por tanto, en general se necesitan ambos diagramas (el m’odulo y la fase) para representar gr’aficamente a F(ω).
 010101
010101 , que s’i genera una señal peri’odica. A
esta secuencia se la conoce por ello como la peor secuencia posible [1],
porque genera la señal digital con periodo m’as corto y por tanto con la
componente de frecuencia fundamental ω0 m’as alta. N’otese que s’olo si
la señal es peri’odica se puede hablar de frecuencia fundamental.
, que s’i genera una señal peri’odica. A
esta secuencia se la conoce por ello como la peor secuencia posible [1],
porque genera la señal digital con periodo m’as corto y por tanto con la
componente de frecuencia fundamental ω0 m’as alta. N’otese que s’olo si
la señal es peri’odica se puede hablar de frecuencia fundamental.
2 muestra gr’aficamente c’omo ser’ia el proceso de aproximaci’on mediante la serie de Fourier para la señal digital que representa a la peor secuencia posible, que anal’iticamente consiste en
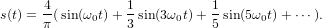 | (6) |
3 donde ωn = 2πfn es la n-’esima componente de frecuencia de s(t) expresada en radianes por segundo (fn se mide por tanto en Hercios o Hz)1 [2, 3].
[1] Fred Halsall. Comunicaciones de Datos, Redes de Computadores y Sistemas Abiertos (4a Edici’on). Pearson Educaci’on, 1998.
[2] B.P. Lathi. Introducci’on a la Teor’ia y Sistemas de Comunicaci’on. Limusa Noriega Editores, 1994.
[3] A.V. Oppenheim and R.W. Shafer. Discrete-Time Signal Processing. Prentice-Hall, 1989.