Contents

1 La función impulso unitario (delta de Dirac)

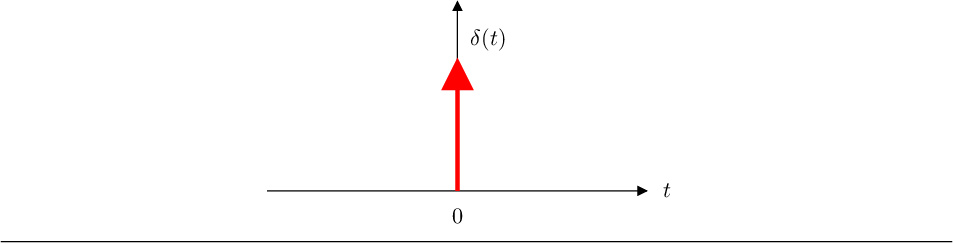
• La función impulso unitario [2] juega un papel determinante en la teoría de la comunicación de señales y en concreto en el teorema del muestreo. Se define como:

  

  y cumple que (delta_1)

  $$\left\{\begin{array}{cc}{\int \; <!--nolimits-->}_{-\infty }^{\infty }\delta \left(t\right)dt=1\hfill & \text{si }t=0\hfill \\ 0\hfill & \text{resto,}\hfill \end{array}\right.$$

  (delta_1)

  es decir, que aunque se trate de un pulso infinitamente estrecho, tiena un area de 1 porque posee una amplitud infinita. Por el mismo motivo se tiene, por definición, que (delta_2)

  $${\int \; <!--nolimits-->}_{-\infty }^{\infty }\delta \left(t\right)f\left(t\right)dt=f\left(0\right){\int \; <!--nolimits-->}_{-\infty }^{\infty }\delta \left(t\right)dt=f\left(0\right),$$

  (delta_2)

  y de la misma forma, que

  $${\int \; <!--nolimits-->}_{-\infty }^{\infty }\delta \left(t-t_0\right)f\left(t\right)dt=f\left(t_0\right).$$

• En virtud de estas definiciones podríamos decir que la función impulso unitario es capaz de calcular el valor de una función en el punto en que se aquella (la delta) se define.

1.1 Obtención de la función impulso unitario

• La función impulso unitario es una función físicamente imposible de generar y que se obtiene en el límite de otras funciones:
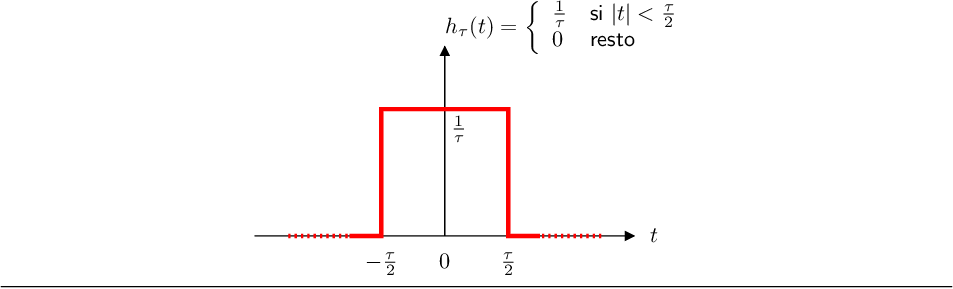
  1. A partir de una función rectangular:

     

     tomando

     $$\underset{\tau \to 0}{lim}{h}_{\tau }\left(t\right)=\delta \left(t\right).$$

  2. A partir de la función muestreo (delta_muestreo):

     $$\delta \left(t\right)=\underset{\tau \to \infty }{lim}\frac{\tau }{\pi }\mathrm{\text{Sinc}}\left(\tau t\right).$$

     (delta_muestreo)

     Nótese que cuando $\tau$ aumenta, la función muestreo se compacta en $t=0$.

2 Transformada de Fourier de la función impulso unitario

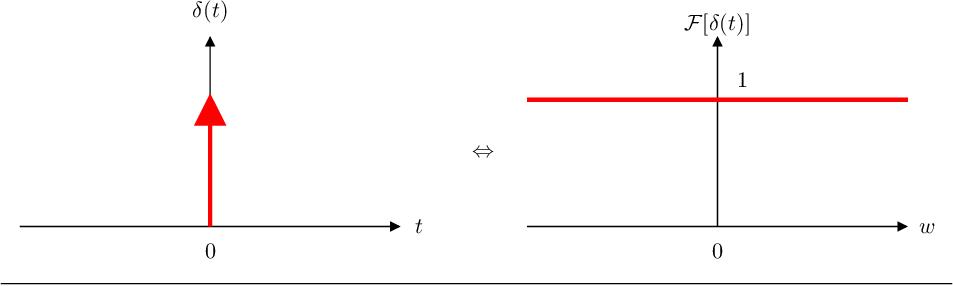
• La transformada de Fourier de la función impulso unitario es $1$. Es decir (FT$\delta$),

  $$\mathcal{ℱ}\left[\delta \left(t\right)\right]=1.$$

  (FT$\delta$)

  Gráficamente:

  

Demostración

Por definición de la transformada de Fourier (véase la Ecuación ??) se tiene que:

3 Transformada de Fourier de una función constante

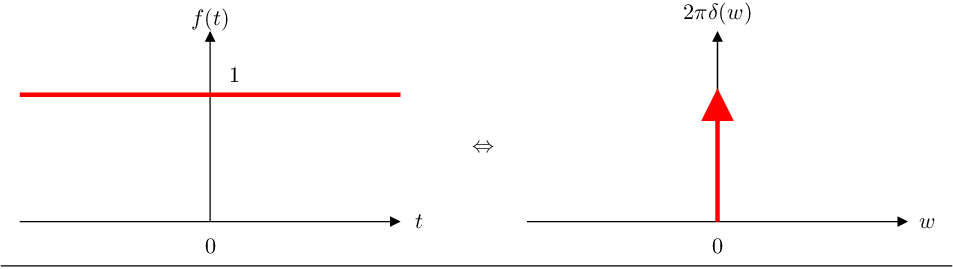
• La transformada de Fourier de la función constante $1$ es la función impulso, multiplicada por $2\pi$. Es decir (Ftcf),

  $$\mathcal{ℱ}\left[1\right]={\int \; <!--nolimits-->}_{-\infty }^{\infty }{e}^{-jwt}dt=2\pi \delta \left(w\right).$$

  (Ftcf)

  Gráficamente:

  

Demostración

• Como sabemos, la transformada de Fourier de una función rectangular es la función Sinc (véase la Sección ??), es decir

  $$\mathcal{ℱ}\left[g_{\tau }\left(t\right)\right]=\tau \mathrm{\text{Sinc}}\left(\frac{\tau }{2}w\right).$$

• Por otra parte, la función rectangular tiende a convertirse en una función constante cuando $\tau \to \infty$, es decir

  $$\underset{\tau \to \infty }{lim}{g}_{\tau }\left(t\right)=1.$$

• En consecuencia, la transformada de Fourier de la función constante $1$ es la transformada de Fourier de una función rectangular $g_{\tau }\left(t\right)$, cuando $\tau \to \infty$, es decir
  $$\begin{array}{ccc}\hfill \mathcal{ℱ}\left[1\right]& \hfill =\hfill & \underset{\tau \to \infty }{lim}\tau \mathrm{\text{Sinc}}\left(\frac{\tau }{2}w\right)=\hfill \\ \hfill & \hfill \hfill & \hfill \\ \multicolumn{3}{c}{\text{(multiplicando y diviendo por }2\pi \text{)}}\\ \hfill & \hfill \hfill & \hfill \\ \hfill & \hfill =\hfill & 2\pi \underset{\tau \to \infty }{lim}\frac{\tau }{2\pi }\mathrm{\text{Sinc}}\left(\frac{\tau }{2}w\right)\hfill \\ \hfill & \hfill \hfill & \hfill \\ \multicolumn{3}{c}{\text{(aplicando la Expresión }\text{delta\_muestreo<!--tex4ht:ref: eq:delta\_muestreo -->}\text{ para }\frac{\tau }{2}\text{)}}\\ \hfill & \hfill \hfill & \hfill \\ \hfill & \hfill =\hfill & 2\pi \delta \left(w\right).\hfill \end{array}$$

4 Transformada de Fourier de la función exponencial compleja

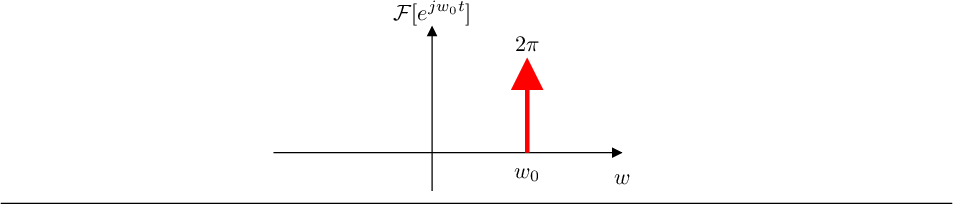
• La transformada de Fourier de la función exponencial compleja de frecuencia $w_0$ es un impulso unitario de energía $2\pi$ en $w_0$ (FTCE),

  $$\mathcal{ℱ}\left[e^{j{w}_{0}t}\right]=2\pi \delta \left(w-w_0\right).$$

  (FTCE)

• Gráficamente:

  

Demostración

Por definición

Si tenemos en cuenta la Ecuación Ftcf y sustituimos para $w=w-w_0$ obtenemos que

5 Transformada de Fourier de la función seno

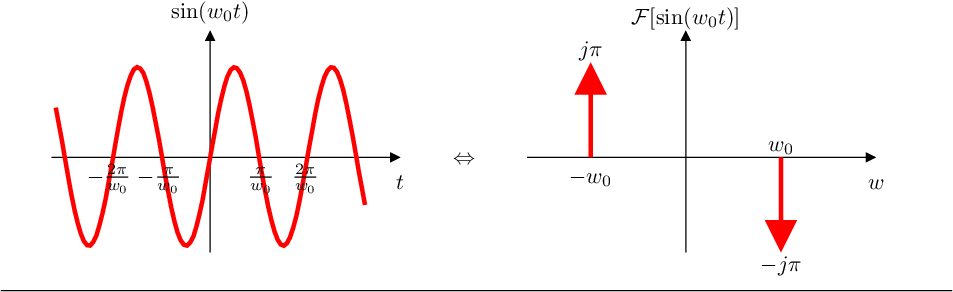
• La transformada de Fourier de la función seno de frecuencia $w_0$ son dos impulsos de energía $j\pi$, uno positivo en $-w_0$ y otro negativo en $w_0$, es decir (FTsin)

  $$\mathcal{ℱ}\left[sin\left(w_{0}t\right)\right]=j\pi \left(\right.\delta \left(w+w_0\right)-\delta \left(w-w_0\right)\left)\right..$$

  (FTsin)

  Gráficamente:

Demostración

Como sabemos,

Por tanto (véase FTCE),

6 Transformada de Fourier de la función coseno

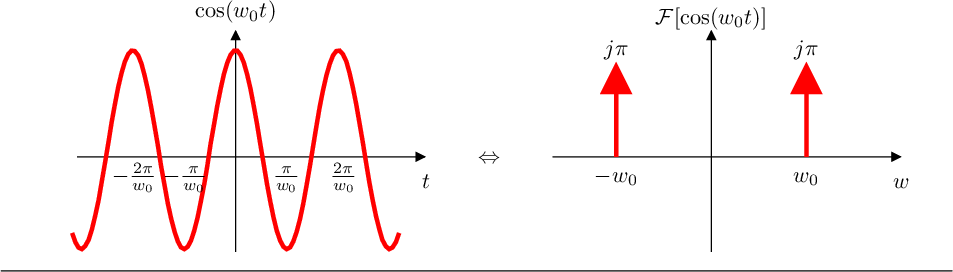
• La transformada de Fourier de la función coseno de frecuencia $w_0$ son dos impulsos positivos de energía $j\pi$, uno en $-w_0$ y otro en $w_0$, es decir (FTCos)

  $$\mathcal{ℱ}\left[cos\left(w_{0}t\right)\right]=j\pi \left(\right.\delta \left(w+w_0\right)+\delta \left(w-w_0\right)\left)\right..$$

  (FTCos)

  Gráficamente:

Demostración

Como sabemos,

Por tanto (véase FTCE),

7 Transformada de Fourier de una función periódica

• Como ya sabemos, podemos expresar cualquier función periódica $f\left(t\right)$ mediante su serie exponencial de Fourier (véase la Ecuación ??)
  $$\begin{array}{cc}\hfill \mathcal{ℱ}\left[f\left(t\right)\right]& =\mathcal{ℱ}\left[\sum _{n=-\infty }^{\infty }{F}_n{e}^{jn{w}_{o}t}\right]\hfill \\ \hfill \\ \hfill & =\sum _{n=-\infty }^{\infty }{F}_n\mathcal{ℱ}\left[e^{jn{w}_{o}t}\right].\hfill \end{array}$$

  Aplicando ahora la Expresión FTCE llegamos a que

  $$\mathcal{ℱ}\left[f\left(t\right)\right]=2\pi \sum _{n=-\infty }^{\infty }{F}_n\delta \left(w-n{w}_0\right).$$

  (Ftpf)

• Esta relación es muy importante porque establece que la función de densidad espectral (la transformada de Fourier) de una señal periódica está compuesta por impulsos localizados en las frecuencias armónicas (frecuencias múltiplos de la frecuencia fundamental $w_0$) de dicha señal, siendo la energía de cada impulso $2\pi$ multiplicado por el valor del coeficiente correspondiente de la serie exponencial de Fourier.
• Gráficamente (para el caso de la función rectangular):

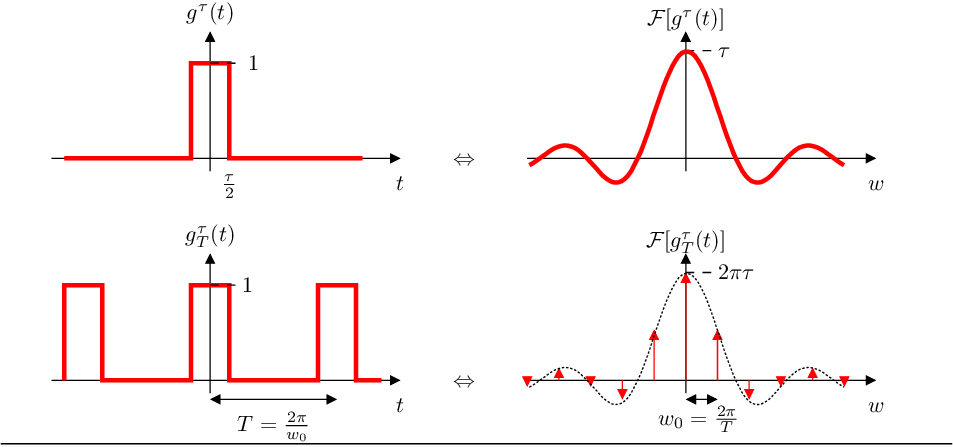
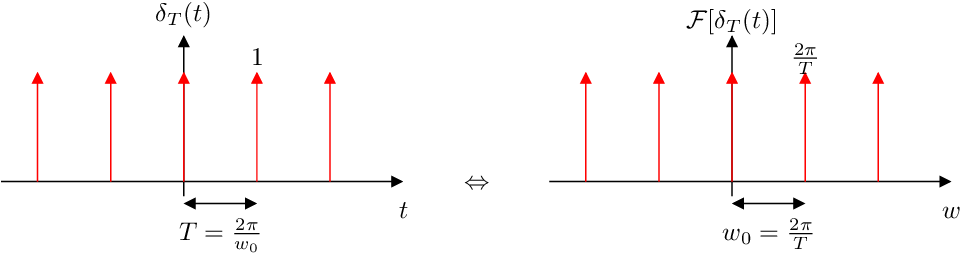
8 Transformada de Fourier de un tren de impulsos unitarios equidistantes

• La función tren de impulsos unitarios equidistantes es muy importante en la teoría del muestreo porque representa matemáticamente el proceso de muestreo de las señales.
• Sea la función tren de impulsos unitarios (${\delta }_T$)

  $${\delta }_T\left(t\right)=\sum _{n=-\infty }^{\infty }\delta \left(t-nT\right).$$

  (${\delta }_T$)

  Entonces, su transformada de Fourier es otro tren de impulsos ($\mathcal{ℱ}\left[{\delta }_T\left(t\right)\right]$)

  $$\mathcal{ℱ}\left[{\delta }_T\left(t\right)\right]=w_0\sum _{n=-\infty }^{\infty }\delta \left(w-n{w}_0\right)=w_0{\delta }_{w_0}\left(w\right).$$

  ($\mathcal{ℱ}\left[{\delta }_T\left(t\right)\right]$)

• Nótese que a medida que $T$ aumenta el espectro se vuelve más denso y decrece su amplitud.

Demostración

• La serie exponencial de Fourier de ${\delta }_T\left(t\right)$ es $${\delta }_T\left(t\right)=\sum _{n=-\infty }^{\infty }{F}_n{e}^{jn{w}_{0}t}$$

  donde recordemos

  $$w_0=\frac{2\pi }{T}$$

  y

  $$F_n=\frac{1}{T}{\int \; <!--nolimits-->}_{-\frac{T}{2}}^{\frac{T}{2}}{\delta }_T\left(t\right)e^{-jn{w}_{0}t}dt.$$

  La función ${\delta }_T\left(t\right)$ en el intervalo $\left(-\frac{T}{2},\frac{T}{2}\right)$ es simplemente $\delta \left(t\right)$. Por tanto

  $$F_n=\frac{1}{T}{\int \; <!--nolimits-->}_{-\frac{T}{2}}^{\frac{T}{2}}\delta \left(t\right)e^{-jn{w}_{0}t}dt.$$

  Por la forma en que se define la función impulso unitario se tiene que

  $$\frac{1}{T}{\int \; <!--nolimits-->}_{-\frac{T}{2}}^{\frac{T}{2}}\delta \left(t\right)e^{-jn{w}_{0}t}dt=\frac{1}{T}{\int \; <!--nolimits-->}_{-\infty }^{\infty }\delta \left(t\right)e^{-jn{w}_{0}t}dt.$$

  Aplicando ahora la definición de la función $\delta \left(t\right)$ (Expresión delta_2) se tiene que

  $$F_n=\frac{e^{jn{w}_{0}0}}{T}{\int \; <!--nolimits-->}_{-\infty }^{\infty }\delta \left(t\right)dt=\frac{1}{T}$$

  y por tanto, que

  $${\delta }_T\left(t\right)=\frac{1}{T}\sum _{n=-\infty }^{\infty }{e}^{jn{w}_{0}t}.$$

  Para encontrar su transformada de Fourier recurrimos a la Ecuación Ftpf. Así llegamos a que

  $$\begin{array}{cc}\hfill \mathcal{ℱ}\left[{\delta }_T\left(t\right)\right]& =2\pi \sum _{n=-\infty }^{\infty }\frac{1}{T}\delta \left(w-n{w}_0\right)\hfill \\ \hfill \\ \hfill & =\frac{2\pi }{T}\sum _{n=-\infty }^{\infty }\delta \left(w-n{w}_0\right)\hfill \\ \hfill \\ \hfill & =w_0\sum _{n=-\infty }^{\infty }\delta \left(w-n{w}_0\right)\hfill \\ \hfill \\ \hfill & =w_0{\delta }_{w_0}\left(w\right).\hfill \end{array}$$

   

9 Transformada de Fourier de una función desplazada en el tiempo

• Si $$\mathcal{ℱ}\left[f\left(t\right)\right]=F\left(w\right)$$

  entonces ($\mathcal{ℱ}\left[f\left(t-t_0\right)\right]$)

  $$\mathcal{ℱ}\left[f\left(t-t_0\right)\right]=F\left(w\right)e^{-jw{t}_0}.$$

  ($\mathcal{ℱ}\left[f\left(t-t_0\right)\right]$)

  Es decir, desplazar una función en el tiempo equivale a multiplicar en el dominio de la frecuencia por la función exponencial compleja.

Demostración

Por definición de transformada de Fourier se tiene que

Sea $x=t-t_0$. Entonces

10 Transformada inversa de Fourier del espectro de una función desplazada en la frecuencia

• Si $$\mathcal{ℱ}\left[f\left(t\right)\right]=F\left(w\right)$$

  entonces ($F\left(w-w_0\right)$)

  $$F\left(w-w_0\right)=\mathcal{ℱ}\left[f\left(t\right)e^{j{w}_{0}t}\right].$$

  ($F\left(w-w_0\right)$)

  Es decir, desplazar el espectro de una función equivale a multiplicar dicha función en el dominio del tiempo por una exponencial compleja.

Demostración

Por definición de transformada de Fourier se tiene que

11 La convolución de funciones

• Sean $f_1\left(t\right)$ y $f_2\left(t\right)$ dos funciones. Su convolución $f_1\left(t\right)\ast f_2\left(t\right)$ se define como ($f_1\left(t\right)\ast f_2\left(t\right)$) [1]

  $$f_1\left(t\right)\ast f_2\left(t\right)={\int \; <!--nolimits-->}_{-\infty }^{\infty }{f}_1\left(\tau \right)f_2\left(t-\tau \right)d\tau .$$

  ($f_1\left(t\right)\ast f_2\left(t\right)$)

Ejemplo

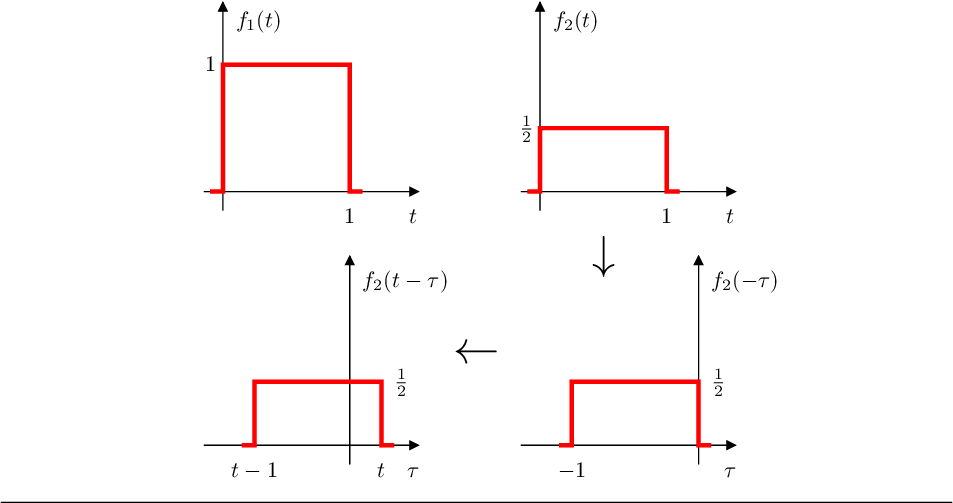
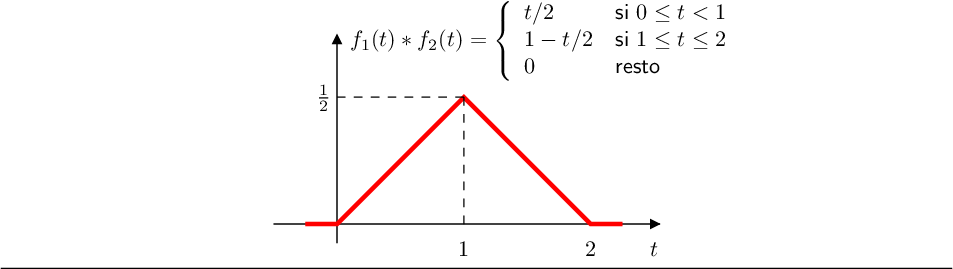
• La convolución de dos funciones $f_1\left(t\right)$ y $f_2\left(t\right)$ se calcula para los distintos valores de $t$ que desplaza a $f_2\left(t-\tau \right)$ en $t$ (segundos) y calculando el area de superposición de las funciones. Así:
  1. Si $t<0$ tenemos el caso:

     

     y como puede apreciarse, no existe solapamiento, es decir $f_1\left(\tau \right)f_2\left(t-\tau \right)=0$.

  2. Si $t=0$:

     

     comienza a existir solapamiento.

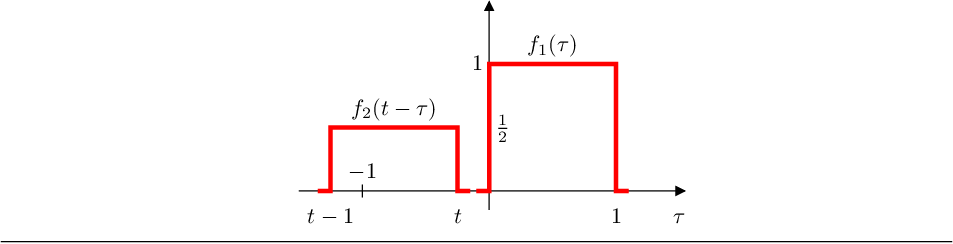
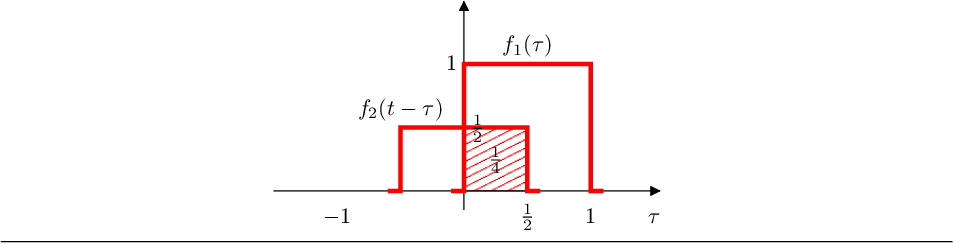
  3. Si $t=1∕2$:

     

     el area de solapamiento es 1/4.

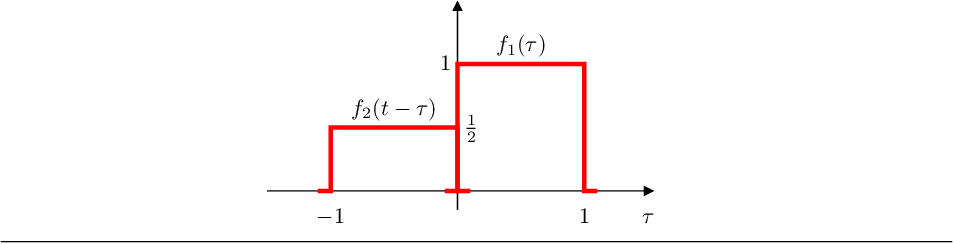
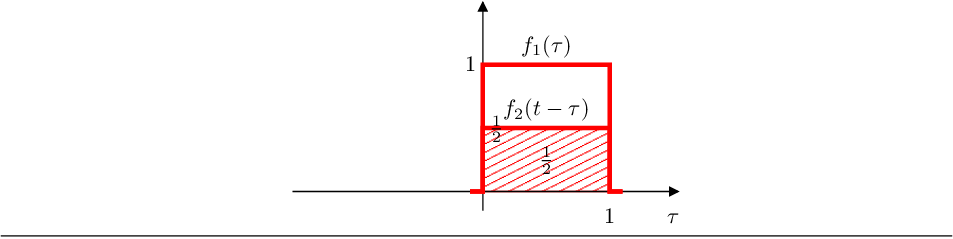
  4. Si $t=1$:

     

     el area es 1/2.

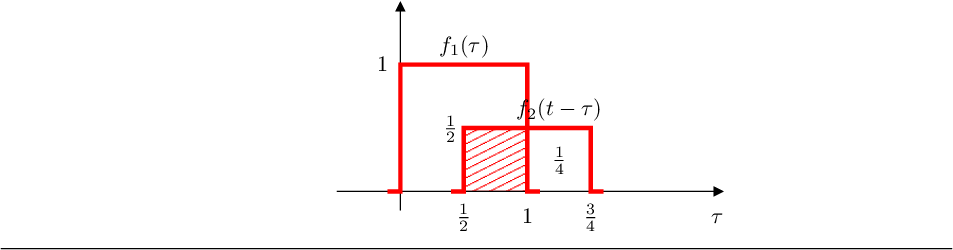
  5. Si $t=3∕4$:

     

     el area de solapamiento es 1/4.

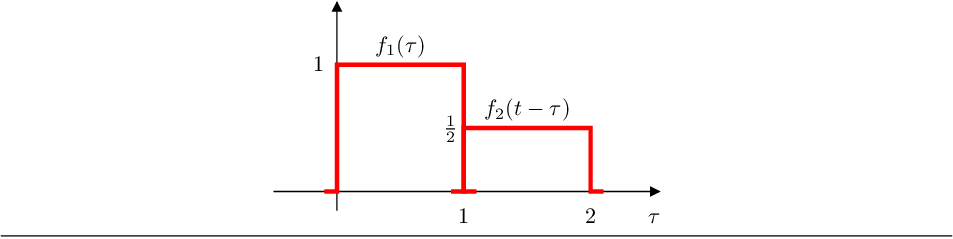
  6. Si $t=2$:

     

     el area de solapamiento vuelve a ser 0.

• Por tanto:

  

12 El teorema de convolución en el dominio del tiempo

• Establece que la convolución de dos funciones $f_1\left(t\right)$ y $f_2\left(t\right)$ en el dominio del tiempo equivale al multiplicar sus espectros $F_1\left(w\right)$ y $F_2\left(w\right)$, es decir (ConvT),

  $$f_1\left(t\right)\ast f_2\left(t\right)={\mathcal{ℱ}}^{-1}\left[F_1\left(w\right)F_2\left(w\right)\right].$$

  (ConvT)

Demostración

Por definición de la transformada de Fourier y de la operación de convolución se tiene que

Nótese que

y aplicando la Expresión $\mathcal{ℱ}\left[f\left(t-t_0\right)\right]$ llegamos a que

Por tanto

13 El teorema de convolución en el dominio de la frecuencia

• Establece que la multiplicación de dos funciones $f_1\left(t\right)$ y $f_2\left(t\right)$ en el dominio del tiempo equivale (salvo por un factor de escala) al convolucionar sus espectros $F_1\left(w\right)$ y $F_2\left(w\right)$, es decir (ConvF),

  $$f_1\left(t\right)f_2\left(t\right)={\mathcal{ℱ}}^{-1}\left[\right.\frac{1}{2\pi }\left(\right.F_1\left(w\right)\ast F_2\left(w\right)\left)\right.\left]\right..$$

  (ConvF)

Demostración

Por definición de la transformada inversa de Fourier (Eq. ??)

Por definición de convolución (Eq. $f_1\left(t\right)\ast f_2\left(t\right)$)

reordenando

Si utilizamos ahora la Eq. $F\left(w-w_0\right)$ y aplicamos la transformada inversa de Fourier llegamos a que

Por tanto, sustituyendo esta expresión en la ecuación anterior tenemos que

reordenando

aplicando, de nuevo, la transformada inversa de Fourier (Eq. ??)

14 Convolución de una función con la función impulso unitario

La convolución de una función $f\left(t\right)$ con la función impulso unitario $\delta \left(t\right)$ resulta en la misma función $f\left(t\right)$. Es decir,

Demostración

Como sabemos, por el teorema de convolución en el tiempo

También sabemos de la Eq. FT$\delta$ que $\Delta \left(w\right)=1$, por lo que necesariamente

15 Convolución con la función impulso unitario desplazada

• La convolución de una función $f\left(t\right)$ con la función impulso unitario desplazada en el tiempo $\delta \left(t-t_0\right)$ resulta la misma función $f\left(t\right)$ desplazada en el tiempo. Es decir ($f\left(t\right)\ast \delta \left(t-t_0\right)$),

  $$f\left(t\right)\ast \delta \left(t-t_0\right)=f\left(t-t_0\right).$$

  ($f\left(t\right)\ast \delta \left(t-t_0\right)$)

Demostración

Aplicando el teorema de convolución en el tiempo (Eq. ConvT) y la Eq. $\mathcal{ℱ}\left[f\left(t-t_0\right)\right]$ llegamos a que

References