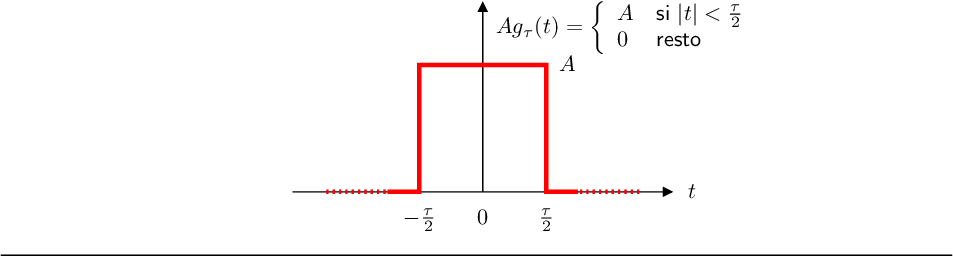
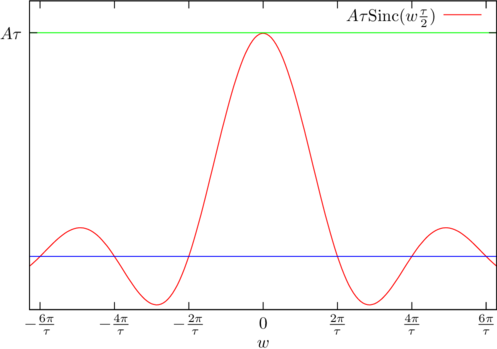
Sean las definiciones (defs_Fes) |
| (defs_Fes) |
siendo .
Si sustituimos dichas definiciones en la Ecuación stf, obtenemos que
Multiplicando llegamos a que
Operando
Aplicando ahora los cambios trigonométricos (e_sin_cos)
|
| (e_sin_cos) |
en la anterior expresión obtenemos que
Operando con el signo de la variable
y deshaciendo parcialmente la sumatoria llegamos a que
Finalmente, juntando las dos sumatorias y el término que quedaba fuera nos
queda que (Fes)
|
| (Fes) |