La Topología es una rama de las matemáticas que podría llamarse "geometría cualitativa", en la que se deja a un lado nociones cuantitativas como longitud, ángulo, área, volumen, y se centra en cuestiones cualitativas como por ejemplo: ¿cuál es el borde de un objeto?, ¿es un objeto conexo, o tiene varias componentes?, ¿tiene agujeros?, ¿está acotado, o tiene partes infinitamente alejadas?, etc. Se basa esencialmente en nociones que tienen que ver con la "proximidad" o la "posición relativa" entre los puntos.

Así, desde el punto de vista topológico, una esfera, un cubo o la superficie de una naranja representan el mismo objeto geométrico, no importa si tiene picos o está arrugado. Es decir, podemos pasar de uno a otro de forma continua. Se dice entonces que son espacios homeomorfos, o que existe un homeomorfismo entre ellos. Es popular el dicho de que un topólogo no distingue entre un donut y una taza de café. Como si de objetos de goma elástica se tratase, podemos doblarlos, estirararlos o encogerlos para pasar de uno a otro. En cambio, no se permite por ejemplo cortar, pegar por puntos distintos o pinchar, porque ello provocaría una discontinuidad.

En fin, la Topología nos proporciona métodos y herramientas que nos permiten distinguir entre espacios no homeomorfos, se dedica al estudio de aquellas propiedades que se conservan a través de homoemorfismos.

A modo de ilustración, veamos algunos ejemplos:

• ¿Cómo distinguiríamos una circunferencia de la unión de dos circunferencias unidas por un punto P? Pues bastaría observar que si quitamos el punto P de dicha unión se rompe en dos pedazos conexos; y sin embargo, si quitamos un punto a una circunferencia quedará sólo un pedazo. En este caso, la propiedad de "conexión" nos permite diferenciar las dos figuras.
• ¿Cómo distinguiríamos por ejemplo el intervalo unidad abierto (0,1) y el intervalo unidad cerrado [0,1]? Aquí veremos que en el primer espacio todos los puntos son "interiores" y sin embargo el segundo posee dos puntos "fronterizos", el 0 y el 1. (La topología de los números reales se estudia ya en un primer curso de cálculo).
• ¿Cómo podríamos distinguir entre una naranja o un donut? Se ve claramente que el segundo tiene un agujero y el primero no, pero ¿cómo los distinguiríamos si hipotéticamente fuésemos habitantes de dos dimensiones ubicados en las superficies de tales espacios. Existen varios métodos para conocerlo. Quizá el más fácil de entender es uno que escuché a José María Montesinos que más o menos decía así: Supongamos que somos de dimensión 2, y que tenemos un perro, por supuesto también de dimensión 2, el cuál hemos atado con una cuerda elástica larga, con un extremo fijo a nuestra casa. Lo dejamos libre un par de días y finalmente vuelve hambriento. En caso de vivir sobre un donut, es bastante probable que vuelva con la correa tirante, tanto más tirante cuantas más vueltas haya dado alrededor del agujero. Sin embargo, en el caso de vivir sobre una naranja es más normal que vuelva con la correa floja (puede que venga con la correa tirante, en caso de que por casualidad haya recorrido una circunferencia máxima sobre la esfera).

Vamos a dar ahora un paseo por algunos de los problemas famosos de la Topología:

El primer problema que dio lugar al nacimiento de la Topología se remonta a 1736, año en el que Euler resuelve el problema de los puentes de Königsberg publicado en un artículo titulado: Solutio problematis ad geometriam situs pertinentis (Solución de un problema relacionado con la geometría de posición).

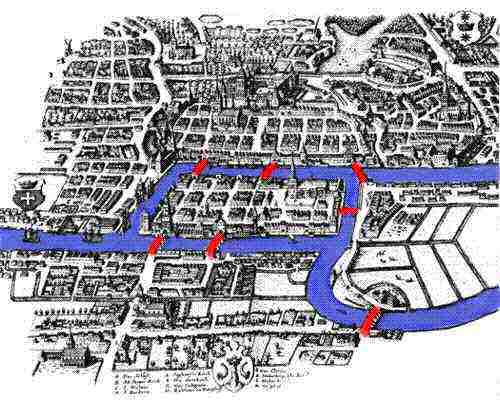
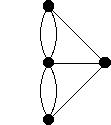
Euler demuestra que es imposible atravesar los siete puentes de Königsberg pasando exactamente una vez por cada uno de ellos. Para ello, traduce el problema en otro en el que intervienen vértices (uno por cada región que podemos caminar a pie) y aristas (una por cada puente).

Se trata pues de encontrar un camino que pase por todas y cada una de las aristas una y sólo una vez, (o, dicho de otro modo, dibujar la figura sin levantar el lápiz del papel). El problema en general tiene solución si y sólo si tal figura contiene como mucho dos vértices con un número impar de aristas. Esto no ocurre en el caso de los puentes de Königsberg. A los figuras con esta propiedad se les llama grafos Eulerianos en el lenguaje actual.

(Recomiendo la lectura de Los puentes de Königsberg, incluido en el libro Cuentos con cuentas de Miguel de Guzmán, Red Olímpica, Buenos Aires, 1997.)

Otro problema interesante que se puede reducir a un problema de grafos, pero en este caso mucho más complicado, es el Problema de los cuatro colores. En 1850. Francis Guthrie, pregunto a su hermano Frederick, en aquel momento estudiante de Augustus de Morgan, el porqué cuatro colores bastaban para colorear cualquier mapa, esto es, sin que dos paises colindantes tuviesen el mismo color. Kenneth Appel y Wolfgang Haken demostraron finalmente en 1976 que sí es posible, reduciendo el problema a un número finito de casos que se resolvieron con la ayuda de un ordenador, el cuál necesitó nada menos que 1200 horas de cálculos.

Páginas web relacionadas:

Cuatro colores bastan, del libro "Cuentos con cuentas", de Miguel de Guzmán.

The four colour theorem

Esta famosa fórmula descubierta por Euler en 1750, relaciona el número de vértices, aristas y caras de un poliedro convexo (o homoemorfo a una esfera). Es curioso que ni Arquímedes ni Descartes la descubrieran, quizás es porque se trata de una fórmula en la que no interviene ninguna magnitud de medida.

Ejercicio: demostrar que los únicos poliedros regulares son el tetraedro, cubo, octaedro, dodecaedro e icosaedro. (Por poliedro regular entendemos que cada cara tiene el mismo número de aristas, y en cada vértice concurren el mismo número de aristas.)

En la fórmula anterior Euler supone que los poliedros son convexos. En general, se tiene que

donde g denota el número de agujeros del poliedro. Descubierta en 1813 por Anoine-Jean Lhuilier (1750-1840), es el primer invariante topológico que se conoce. Por ejemplo, para el toro tenemos v-a+c=0. Se puede concluir entonces que el toro y la esfera no son homeomorfos ya que tienen características de Euler distintas. De igual forma, el doble toro, el triple toro, etc son todas superficies diferentes, ya que tienen características de Euler -2, -4, etc.

 Páginas web relacionadas: El matemático como naturista, del libro "Cuentos con cuentas" de Miguel de Guzmán.

Fórmula de Euler para dimensiones superiores

El toro:

Es la superficie de un donut.

 

 

 

 

La Banda de Möbius:

Seguro que todos hemos construido una cinta de Möbius con papel. A partir de una tira de papel rectangular, unimos con pegamento los dos extremos después de haber girado uno de ellos 180 grados. El resultado es una superficie con una sola cara, con borde una circunferencia y que no es orientable (un supuesto habitante de dimensión dos que viviese en esta superficie podría aparecer después de rodear toda la banda con el corazón en lado izquierdo, o si tuviese un reloj de pulsera, las agujas girarían en sentido contrario al normal). Otra de las propiedades sorprendentes es que al cortarla justo por su meridiano se consigue una sola pieza y no dos como cabría esperar. August Möbius (1790-1868) publica una descripción de esta superficie y sus propiedades más destacables en 1865.

 Páginas web relacionadas: 1, 2, 3

Mathematics in Robinson's sculptures

Es una botella que consta de una sóla cara y que no tiene ni interior ni exterior. En cierto sentido, se obtiene de forma análoga a la banda de Möbius. Empezamos a partir de un cilindro sin tapas y unimos las dos circunferencias de los extremos, no en el sentido usual, que obtendríamos el toro, sino al revés. Es decir, hemos de imaginarnos que uno de los extremos entra dentro del cilindro sin cortarlo (se puede hacer si disponemos de una cuarta dimensión). Otra forma de ver la botella de Klein es uniendo dos bandas de Möbius por su borde.

Páginas web relacionadas: Miscelanea de superficies de L.A. Cordero,

Es claro que una circunferencia contenida en un plano, divide a éste en dos regiones, una interior y otra exterior. Esta propiedad se sigue cumpliendo si deformamos continuamente la circunferencia en un cuadrado o un triángulo, o en general en cualquier curva cerrada que no se corte a sí misma. Este es el famoso Teorema de la curva de Jordan.

Incluyo aquí un extracto del artículo Las Matemáticas ante el cambio de milenio, de Phillip Griffiths, aparecido en The American Mathematical Monthly, número 1 del volumen 107 de Enero de 2000, y posteriormente en La Gaceta de la Real Sociedad Matemática Española Vol.3, nº1, Enero-Abril 2000, pp. 23-41.

"... La conjetura de Poincaré. Este problema es desconcertante porque, a la vez, es muy fundamental y tiene una apariencia muy simple. En los días de Poincaré, hace un siglo, se consideraba como una cuestión trivial al igual que toda la Topología, un área de las Matemáticas que, en esencia, él había inventado. La Topología de hoy en día es un área vital y significativa de las Matemáticas.

Grosso modo, la topología se interesa por las propiedades fundamentales de las estructuras y de los espacios. Desde el punto de vista de un topólogo, se puede estirar, comprimir o torcer una esfera y seguirá siendo una esfera, siempre y cuando no la pinchemos o la rasguemos. Un topólogo ve un donut y una taza de café como la misma cosa, porque puede deformar cualquiera de ellos hasta obtener una forma básica común a ambos, a la que se llama toro. Los topólogos están particularmente interesados en las variedades, nombre que sugiere multiplicidad de formas. Un balón de fútbol, por ejemplo, es una variedad de dimensión 2, una 2-esfera; lo podemos manipular como queramos, pero sin romperlo, y seguirá siendo un balón de fútbol.

El objetivo de los topólogos es identificar todas las variedades posibles, incluyendo la forma del universo, que es el tema de la conjetura de Poíncaré. Esto es relativamente fácil en 2 dimensiones, y se consiguió al final del siglo XIX. El criterio para comprobar si una variedad es una 2-esfera es muy simple. Imagine el lector que coloca una goma elástica en la superficie de un balón de fútbol. Si la goma se puede comprimir (sin salirse de la superficie) hasta ocupar un solo punto, y esto en cualquier parte de la superficie, el balón es una 2-esfera y decimos que es simplemente conexa.

En 1904, Poincaré conjeturó que lo que es válido en 2 dimensiones lo sería también en 3 y que cualquier variedad de dimensión 3 que sea simplemente conexa (como el universo en que habitamos) ha de ser una 3-esfera. Esto parece obvio, pero nadie ha sido capaz hasta ahora de demostrar que no hay 3-esferas espurias, de manera que la conjetura no ha sido resuelta. Por sorprendente que pueda parecer, la conjetura análoga para dimensiones mayores que 3 sí ha sido comprobada, pero la dimensión tres se resiste. "