4.3. CO2 uptake, pH, and inorganic carbon equilibria.

CO2 is the other gas, along with oxygen, we need to deal with.

Carbon dioxide is taken up by the microalgae to form new biomass. Carbon dioxide should be supplied in excess so that it never becomes a bottleneck, otherwise photoinhibition will appear as there will be no acceptors for the e- generated in the water-splitting step taking place in PSII.

Carbon dioxide participates simultaneously is several equilibria with other carbon species. Additionally, CO2 is used as the acidity source needed to compensate for the alcalinity generated during the nitrate metabolism.

So, there are a few thighs taking place all at the same time. Fasten you seat belts.

Questions:

1. • Find the carbon species distribution for pH=7.8 and TIC=0.5 M.
   

2. • How much CO2 can absorb a solution of NaOH 1M untit a pH of 8 is reached?
   

3. • Write the cation balance (last equation) for an alcalinization rate of 1:1 (1 OH- released for each NO3- taken up).
   

1. •Inorganic carbon equilibria.
   

On the first place, CO2 reacts with water to form bicarbonate. The reaction and the equilibrium are the following:

Let K1 be the equilibrium constant:

Where α is the coefficein that relates the concentration of bicarbonate to carbon dioxide. We can work out a simmilar coefficient for carbonate:

Thus:

With this, we can write the following balance for the total inorganic carbon (CT):

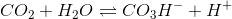
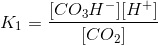
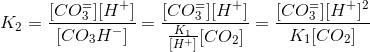
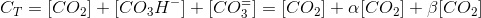
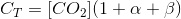
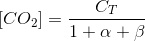
Photosynthesis and carbon uptake.

CO2 is absorbed by microalgae during photosynthesis. We already know the uptake rate:

Or also in differential form:

Since some of the CO2 concentration is restored by the equilibria, be have to balance the total inorganic carbon, not the CO2. But this restoring process consumes H+ ions, rising the pH. We will write a balance for H+ soon.

Inorganic carbon balance in a closed system.

In a closed sytem, the pH, carbon uptake and nitrogen metabolism interact to give a rather complicated set of equations. We will not need this general case but it is illustrative as it shows how the photosynthetic activity can increase pH and make culturing imposible. The equations we need are the following.

The inorganic carbon balance with carbon uptake:

That integrates to:

The nitrate metabolism does not consume carbon but does alter the pH and thus the carbon species distribution. The simplest way to take into account the release of OH- is a balance of charges also known as electroneutrality. Let C+ be the concentration of cations that compensate for the negative charge of the carbon species an the water ionization. This is:

Therefore:

Which is a sole function of the total inorganic carbon and the pH, as α and β are functions only of pH. At the begining of the culture time (t=0) we have CT0 and pH0:

The reduction of nitrate changes 1 NO3- for 7 OH-. C+ is then increased:

The electroneutrality is unnafected by any increase of CT due to CO2 addition since this is a neutral substance. The adition the CO2 only increases CT. Substituting an reagrupating, the balance results:

Which gives the evolution of pH with the increase in biomass (Cb(t)).

pH and nitrate metabolism.

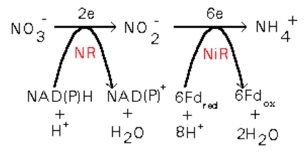
Another process that can consume a substantial amount of H+ is the reduction of nitrate to amine (-NH2), the form fund in proteins. This process consumes seven H+ (the picture shows the conversion of nitrate to ammonium, which releases two H+ when incorporated as an amine group, 1-8-2=7). These H+ are obtained from water molecules, that are turned into OH-.

If we call XN to the nitrogen content of the biomass (mass fraction, g g-1), we have:

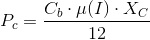
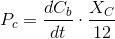
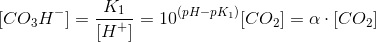
The common practice is to compensate this alkalnization by transferring more CO2 to the culture. This additional CO2 will consume OH- ions turning them into bicarbonate and cabonate. Thus, we will have t include this in the CO2 needs of the culture.

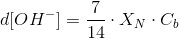
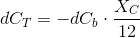
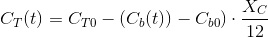
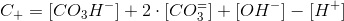
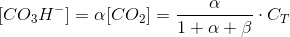
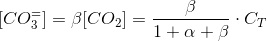
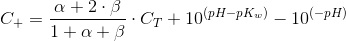
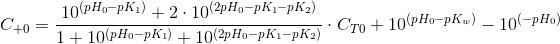
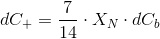
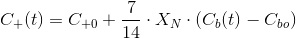
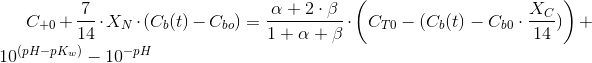
Which is a very convenient form to calculate the CO2 concentration. We warned thet y used bracket cocncentrations because it is the standard form to write equilibrium constants. Later on you will finf CCO2 instead of [CO2].

Knowing that at 25ºC, pK1=6.35, pK2=10.33 and pKw=13.995, calculate α and β at pH=7 and pH=8.

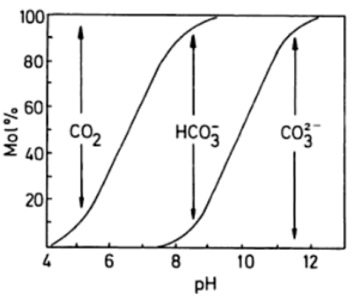
If you calculate the relative concentrations of each carbon species at different pH, you will get a plot as the one shown on the right. Nothe that at pH=8 is bicarbonate the dominating species but there is still a substantial proportion of carbon dioxide. You can now calculate the exact figure.