NOCIONES BÁSICAS

DEFINICIONES Un subconjunto A de puntos del plano se dice que es convexo si para cualesquiera dos puntos de A, el segmento que los une está contenido en A. Dado B, un subconjunto de puntos del plano. Se llama Cierre Convexo (también conocido como Envolvente Convexa o Convex Hull) al menor conjunto convexo del plano que conriene a B.  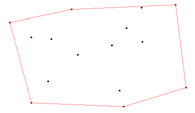    De forma intuitiva sería como si en cada punto de B claváramos una púa y las rodeáramos por una cinta elástica estirada. Cuando la cinta se contrayera, ésta tomaría la forma del cierre convexo. Aunque usualmente se mencionan refiriéndose a la misma cosa, es interesante puntualizar la diferencia entre Cierre Convexo y Envolvente Convexa. Cuando hablamos de Cierre Convexo nos estamos refiriendo a una región cerrada que incluye todos los puntos del interior del conjunto, mientras que cuando hablamos de Envolvente Convexa hablamos de la frontera de esa región. Se denominan puntos extremos a los vértices de la envolvente convexa. PLANTEAMIENTO DEL PROBLEMA El problema de calcular el cierre convexo se puede dividir en dos frentes: Dado un conjunto de puntos del plano, encontrar aquellos que sean vértices del cierre convexo. Dado un conjuto de puntos del plano, encontrar una descripción de la frontera del cierre, es decir, encontrar el polígono que forma la envolvente convexa. En los algoritmos que se van a mostrar responderemos a dicho problema de un modo intermedio. Por un lado la salida serán los vértices del cierre convexo, pero por otro lado, dichos vértices estarán ordenados, de forma que sea sencillo construior el polígono.