Construcción Geométrica de Cuaternas Armónicas
Curso Interactivo sobre Geometría Proyectiva
Definición 0.1 Una cuaterna de puntos sobre la recta proyectiva
se dice cuaterna armónica si su razón doble es igual a![]() .
.
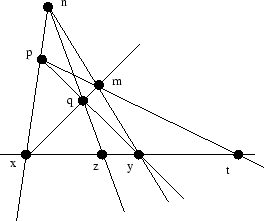
Teorema 0.1 En la figura siguiente la cuaterna ![]() es armónica.
es armónica.
Ejercicio 0.1 (05) Hallar en la figura dos transformaciones
perspectivas tal que su
composición intercambia ![]() e
e ![]() y fijando
y fijando ![]() y
y ![]() .
.
Ejercicio 0.2 (05) Usar que las perspectivas conservan razones
dobles para deducir el teorema del ejercicio anterior.