Primera sesión: 11,30 horas
Aproximantes de Bernstein y de tipo Bernstein
Teresa E. Pérez Fernández. Universidad de Granada
Resúmen En 1912, S. Bernstein publicó la primera demostración constructiva del teorema de K. Weierstrass, quien probó veinte años antes la aproximación uniforme por polinomios de funciones reales y continuas definidas sobre un intervalo cerrado y acotado. S. Bernstein demuestra el resultado anterior utilizando los actualmente llamados polinomios (o aproximantes) de Bernstein. Utilizando la idea de Bernstein, estos polinomios han sido modificados por diversos autores. La idea suele ser la obtención de aproximantes para funciones definidas en intervalo acotado o no que verifiquen ciertas propiedades adicionales, entre las que podríamos destacar las relaciones con los polinomios ortogonales clásicos.
Segunda sesión: 12,30 horas
Introducción a la aproximación en norma de Hölder
Dr. D. Miguel Jiménez Pozo. Profesor Investigador de la Benemérita Universidad Autónoma de Puebla, México y Catedrático Invitado de la Universidad de Jaén, España.
Resúmen Si ![]()
![]() es un
intervalo real y
es un
intervalo real y ![]()
![]() , el espacio de
Hölder
, el espacio de
Hölder ![]()
![]() es el espacio
lineal de aquellas funciones
reales o complejas y
uniformemente acotadas
es el espacio
lineal de aquellas funciones
reales o complejas y
uniformemente acotadas ![]()
![]() sobre
sobre ![]()
![]() , para
las cuales
, para
las cuales
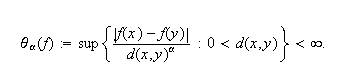
El espacio ![]()
![]() es de Banach con
la norma
es de Banach con
la norma ![]()
![]() u
otra equivalente y contiene,
en particular, los polinomios
algebraicos o los
trigonométricos en el caso
periódico. Luego todos
aquellos problemas clásicos
concernientes a la mejor
aproximación polinomial,
módulos de continuidad y
k-funcionales de diferentes
órdenes, problemas directos
e inversos tipo Jackson y Bernstein, convergencia de
las series de Fourier, etc.,
pueden formularse en estos
espacios de manera natural.
En esta charla se recopilan
los principales resultados
existentes en la temática,
incluyendo sus origenes,
motivaciones y principales
extensiones a otros espacios
tales como los de Besov.
u
otra equivalente y contiene,
en particular, los polinomios
algebraicos o los
trigonométricos en el caso
periódico. Luego todos
aquellos problemas clásicos
concernientes a la mejor
aproximación polinomial,
módulos de continuidad y
k-funcionales de diferentes
órdenes, problemas directos
e inversos tipo Jackson y Bernstein, convergencia de
las series de Fourier, etc.,
pueden formularse en estos
espacios de manera natural.
En esta charla se recopilan
los principales resultados
existentes en la temática,
incluyendo sus origenes,
motivaciones y principales
extensiones a otros espacios
tales como los de Besov.
Primera Sesión: 11,30 horas
Polinomios ortogonales de Freud--Sobolev
Juan José Moreno Balcázar. Universidad de Almería.
Resúmen En esta charla se
presenta una generalización
de los denominados polinomios
ortogonales de Freud
asociados a la función peso ![]()
![]() en la recta real.
Para empezar se recuerda
brevemente algunas
propiedades de estos
polinomios de Freud, así
como referencias históricas.
A continuación, se introduce
el producto escalar de Sobolev:
en la recta real.
Para empezar se recuerda
brevemente algunas
propiedades de estos
polinomios de Freud, así
como referencias históricas.
A continuación, se introduce
el producto escalar de Sobolev:
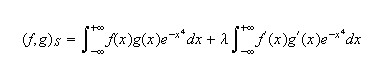
donde ![]()
![]() y se aborda el
objetivo principal de la
charla, que no es otro que
presentar algunas propiedades
asintóticas de los
polinomios ortogonales con
respecto al producto escalar
().
y se aborda el
objetivo principal de la
charla, que no es otro que
presentar algunas propiedades
asintóticas de los
polinomios ortogonales con
respecto al producto escalar
().
Segunda sesión: 12,30 horas
Una generalización parcial del teorema de alternancia de Chebyshev
Dr. D. Miguel Jiménez Pozo. Profesor Investigador de la Benemérita Universidad Autónoma de Puebla, México y Catedrático Invitado de la Universidad de Jaén, España.
Resúmen Sea ![]()
![]() el
intervalo real
el
intervalo real ![]()
![]() y
y ![]()
![]() funciones reales
continuas sobre
funciones reales
continuas sobre ![]()
![]() , donde
, donde
![]()
![]() y
y ![]()
![]() son
estrictamente positivas.
Definimos
son
estrictamente positivas.
Definimos
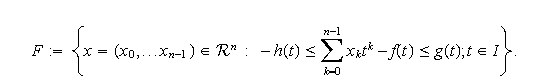
El conjunto ![]()
![]() es
convexo, compacto y puede ser
vacío, tan grande que su
interior sea no vacío, o
simplemente reducido a un
punto. De estas tres
posibilidades, el último
caso queda caracterizado de
varias formas, de la cual la
más relevante es la
existencia de
es
convexo, compacto y puede ser
vacío, tan grande que su
interior sea no vacío, o
simplemente reducido a un
punto. De estas tres
posibilidades, el último
caso queda caracterizado de
varias formas, de la cual la
más relevante es la
existencia de ![]()
![]() puntos
puntos ![]()
![]() , en
los cuales el error de
aproximación
, en
los cuales el error de
aproximación
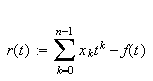
alcanza su módulo máximo y
lo hace alternando el signo
consecutivamente. Este
teorema generaliza
parcialmente el famoso
teorema de Chebyshev de
finales del siglo XIX sobre
la caracterización del
elemento de la mejor
aproximación uniforme, en el
cual
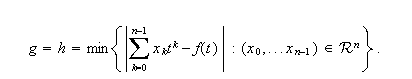
Este resultado se extiende al
caso en el cual los
polinomios algebraicos son
sustituidos por un sistema de Haar.
Primera sesión: 12,00 horas
Hermite-Pade approximants and Nikishin systems in diophantine theory and theory of dinamical systems.
Vladimir N. Sorokin
Resúmen: This talk is a survey of some results on this subject. We investigate asymptotic behavior of Hermite-Pade approximants for arbitrary graphs of Markoff functions. We prove the linear independence of values of generalized polylogarithms and estimate transcendentness mesuare for the number pi. We integrate also a nonlinear dynamical system in terms of continued fractions.
Primera sesión: 11,30 horas
Sobre cierta modificación de un
funcional de momentos
Dr. D. Manuel Alfaro García. Universidad
de Zaragoza.
Resúmen: Dado un funcional de momentos
cuasidefinido (o regular) 
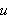 sobre el espacio de los polinomios de Laurent
se considera el funcional
sobre el espacio de los polinomios de Laurent
se considera el funcional
![]()
donde 
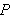 es un polinomio complejo.
es un polinomio complejo.
Se estudia el carácter cuasidefinido del
funcional 
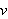 y, en esa situación, se relacionan las
sucesiones de polinomios ortogonales sobre la
circunferencia unidad asociadas a
y, en esa situación, se relacionan las
sucesiones de polinomios ortogonales sobre la
circunferencia unidad asociadas a 
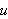 y
y 
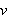 .
.
Segunda sesión: 12,30 horas
Propiedades asintóticas de los
polinomios de Laguerre--Sobolev
Dra. Dña. María Luisa Rezola Solaun.
Universidad de Zaragoza.
Resúmen Sean 
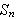 los polinomios ortogonales respecto del
producto
los polinomios ortogonales respecto del
producto
![]()
donde
![]()
con 
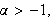

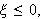

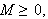 y
y 
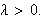
Se estudian diversas propiedades asintóticas
para estos polinomios 
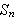 como: asintótica fuerte en
como: asintótica fuerte en 
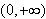 ,
una fórmula tipo Mehler-Heine y una asintótica
exterior tipo Plancherel-Rotach. Como
consecuencia se obtendran diversos resultados
sobre los ceros de
,
una fórmula tipo Mehler-Heine y una asintótica
exterior tipo Plancherel-Rotach. Como
consecuencia se obtendran diversos resultados
sobre los ceros de 
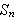 .
.